$(a+b)^2$ formula
Formula
$(a+b)^2 \,=\, a^2+2ab+b^2$
Basically, $(a+b)^2$ is an algebraic expression that represents the square of a sum. It is one of the most important identities in algebra, and its expansion is widely used as a fundamental formula to simplify expressions and solve equations in mathematics.
What is the (a + b)² Formula?
When $a$ and $b$ are algebraic variables, adding them gives their sum, $a+b$. Squaring this sum produces $(a+b)^2$, which is called the square of a sum.
The algebraic expression $(a+b)^2$ is read mathematically as
- $a$ plus $b$ squared
- $a$ plus $b$ whole square
- Square of $a$ plus $b$
- Square of the sum of $a$ and $b$
All four names have the same meaning, and you can use any of them to express $(a+b)^2$ in mathematics.
In mathematics, $(a+b)^2 \,=\, a^2+2ab+b^2$. Therefore, $a^2+2ab+b^2$ is called the expansion of $(a+b)^2$.
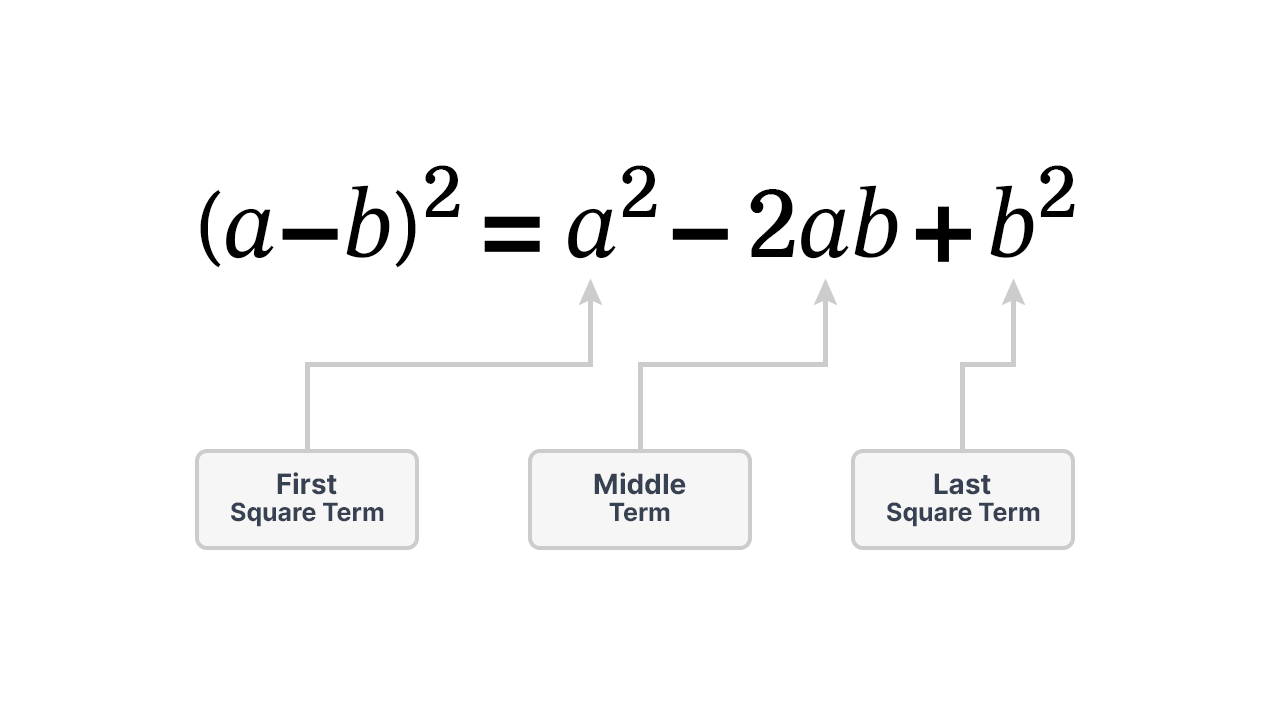
- The term $a^2$ is called the first square term, or the square of the first term.
- The term $2ab$ is called the middle term, or cross term, or twice the product of the two terms.
- The term $b^2$ is called the second square term, or the square of the second term.
How to Read (a + b)2 Formula in Algebra
$(a+b)^2 \,=\, a^2+2ab+b^2$
$a$ plus $b$, squared, equals $a$ squared plus two $a$ $b$ plus $b$ squared.

Verification of the (a+b)² Formula
Before using the $a$ plus $b$ squared formula in mathematics, it is important to verify that it is correct. This can be done using simple numerical examples.
Example
Substitute $a = 3$ and $b = 4$ into both sides of the $(a+b)^2$ formula.
- $(a+b)^2$ $\,=\,$ $(3+4)^2$ $\,=\,$ $7^2$ $\,=\,$ $49$
- $a^2+2ab+b^2$ $\,=\,$ $3^2+2(3)(4)+4^2$ $\,=\,$ $9+24+16$ $\,=\,$ $49$
$\,\,\,\,\therefore\,\,\,\,$ $(a+b)^2$ $\,=\,$ $a^2+2ab+b^2$ $\,=\,$ $49$
You can verify the square of $a$ plus $b$ formula using any two numbers and confirm that it is always correct. Therefore, it is known as the $(a+b)^2$ identity in algebra.
How to Use the (a + b)² Formula
The square of the sum of $a$ and $b$ is widely used in algebra and problem-solving in two important ways in mathematics. Let us know each case with clear and understandable examples.
Expansion
The $a$ plus $b$ whole square is expanded as $a$ squared plus two $a$ $b$ plus $b$ squared.
$\implies$ $(a+b)^2$ $\,=\,$ $a^2+2ab+b^2$
This expansion is used as a formula when an expression is already written as the square of a sum (a binomial).
Example
Expand $(1+4)^2$
Substitute $a = 1$ and $b = 4$ into the $(a+b)^2$ formula.
$=\,\,$ $1^2$ $+$ $2(1)(4)$ $+$ $4^2$
$=\,\,$ $1^2$ $+$ $2 \times 1 \times 4$ $+$ $4^2$
$=\,\,$ $1+8+16$
$=\,\,$ $25$
Example
Expand $(5x+2)^2$
Substitute $a = 5x$ and $b = 2$ into the $(a+b)^2$ formula.
$=\,\,$ $(5x)^2$ $+$ $2(5x)(2)$ $+$ $2^2$
$=\,\,$ $(5x)^2$ $+$ $2 \times 5x \times 2$ $+$ $2^2$
$=\,\,$ $25x^2+20x+4$
Example
Expand $(3x+7y)^2$
Substitute $a = 3x$ and $b = 7y$ into the $(a+b)^2$ formula.
$=\,\,$ $(3x)^2$ $+$ $2(3x)(7y)$ $+$ $(7y)^2$
$=\,\,$ $(3x)^2$ $+$ $2 \times 3x \times 7y$ $+$ $(7y)^2$
$=\,\,$ $9x^2+42xy+49y^2$
Example
Expand $\bigg(2x+\dfrac{3y}{5}\bigg)^2$
Substitute $a = 2x$ and $b = \dfrac{3y}{5}$ into the $(a+b)^2$ formula.
$=\,\,$ $(2x)^2$ $+$ $2(2x)\bigg(\dfrac{3y}{5}\bigg)$ $+$ $\bigg(\dfrac{3y}{5}\bigg)^2$
$=\,\,$ $(2x)^2$ $+$ $2 \times 2x \times \dfrac{3y}{5}$ $+$ $\bigg(\dfrac{3y}{5}\bigg)^2$
$=\,\,$ $4x^2$ $+$ $\dfrac{2 \times 2x \times 3y}{5}$ $+$ $\dfrac{9y^2}{25}$
$=\,\,$ $4x^2$ $+$ $\dfrac{12xy}{5}$ $+$ $\dfrac{9y^2}{25}$
The above example explains how a binomial in the form of the square of a sum is expanded step by step into a three-term expression using the $a+b$ whole square formula.
Factorization
The expression $a^2+2ab+b^2$ is called a perfect square trinomial, and it can be easily factorized as the square of the sum of two terms, $(a+b)^2$, using this important algebraic identity.
$\implies$ $a^2+2ab+b^2$ $\,=\,$ $(a+b)^2$
The three-term expression can be factored using the $a$ plus $b$ whole square formula.
Example
Simplify $16p^2-40pq+25q^2$
The given expression has three terms. The first and last terms are squares, and the middle term is negative. So, it can be written as the square of a difference using the $a-b$ squared formula.
$=\,\,$ $(4p)^2$ $-$ $2 \times (4p) \times (5q)$ $+$ $(5q)^2$
$=\,\,$ $(4p)^2$ $-$ $2(4p)(5q)$ $+$ $(5q)^2$
$=\,\,$ $(4p-5q)^2$
The above example demonstrates how to factor a trinomial whose first and last terms are perfect squares and whose middle term is $-2ab$ into the square of a difference using the $a$ minus $b$ whole square formula.
The above two simple examples show how to use the $a$ minus $b$ squared formula in mathematics.
Common Mistakes in (a−b)² Formula
Students often make mistakes while expanding $(a-b)^2$, especially when handling the middle term. The following points highlight the most common errors to help you avoid them and apply the formula correctly.
- Writing $(a − b)^2 \,=\, a^2 − b^2$
- Forgetting the middle term $−2ab$
Why is the (a − b)² formula important?
This identity is used in factorization, completing the square, solving quadratic equations, and understanding area models in geometry. It helps simplify expressions and solve problems efficiently in mathematics.
Other Forms of the Formula
In mathematics, the square of a difference formula can be written using different variables such as $x$ and $y$ instead of $a$ and $b$. Therefore, $(a-b)^2$ and $(x-y)^2$ represent the same square of a difference formula, with only the variables changing.
Formula
$(x-y)^2$ $\,=\,$ $x^2-2xy+y^2$
You have learned what the $(a-b)^2$ formula is and how it is used in mathematics, including arithmetic verification to check its correctness. Next, we will learn how to derive the $(a-b)^2$ algebraic identity clearly and step by step in two different methods.
