$(a+b)^3$ formula

Formula

$(a+b)^3$ $\,=\,$ $a^3+b^3+3ab(a+b)$

Introduction

Let $a$ and $b$ be two variables, which are considered to represent two terms in algebraic form. The sum of the both terms is written as $a+b$ in mathematics. It is not only an algebraic expression and also a binomial. The cube of sum of the terms $a$ and $b$ or a binomial is written in the following mathematical form in mathematics.

$(a+b)^3$

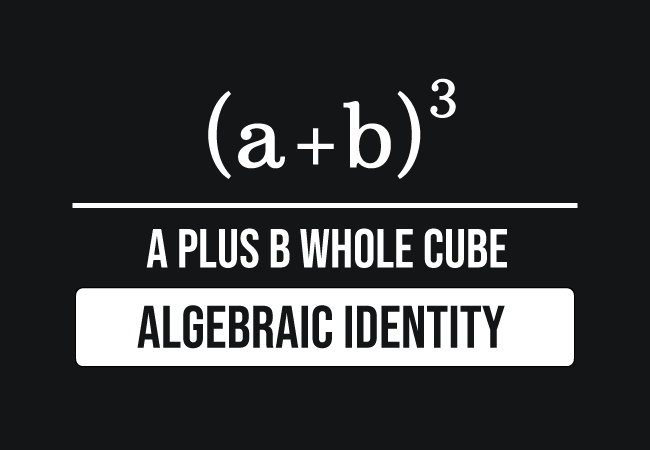
The $a$ plus $b$ whole cube is equal to the $a$ cubed plus $b$ cubed plus three times the product of $a$, $b$ and sum of $a$ plus $b$.

$(a+b)^3$ $\,=\,$ $a^3+b^3+3ab(a+b)$

The cube of $a$ plus $b$ is also equal to the $a$ cubed plus $b$ cubed plus three times product of $a$ squared and $b$ plus $3$ times product of $a$ and $b$ squared.

$\implies$ $(a+b)^3$ $\,=\,$ $a^3+b^3+3a^2b+3ab^2$

In mathematics, the $a$ plus $b$ whole cubed algebraic identity is called in the following three ways.

1. The cube of sum of two terms rule.
2. The cube of a binomial identity.
3. The special binomial product formula.

Usage

In mathematics, the cube of the sum of two terms rule is used as a formula in the following two cases.

Expansion

The cube of the sum of two terms is expanded as the sum of cubes of both terms and three times the product of both terms and sum of them.

$\implies$ $(a+b)^3$ $\,=\,$ $a^3+b^3+3ab(a+b)$

Simplification

The sum of cubes of both terms and three times the product of both terms and sum of them is simplified as the cube of the sum of two terms.

$\implies$ $a^3+b^3+3ab(a+b)$ $\,=\,$ $(a+b)^3$

Examples

$(1) \,\,\,$ Find $(2x+3y)^3$

Now, take $a = 2x$ and $b = 3y$ and substitute them in the expansion of the cube of sum of two terms formula for expanding it.

$\implies$ $(2x+3y)^3$ $\,=\,$ $(2x)^3$ $+$ $(3y)^3$ $+$ $3(2x)(3y)(2x+3y)$

$\implies$ $(2x+3y)^3$ $\,=\,$ $8x^3$ $+$ $27y^3$ $+$ $18xy(2x+3y)$

$\implies$ $(2x+3y)^3$ $\,=\,$ $8x^3$ $+$ $27y^3$ $+$ $18xy \times 2x$ $+$ $18xy \times 3y$

$\implies$ $(2x+3y)^3$ $\,=\,$ $8x^3$ $+$ $27y^3$ $+$ $36x^2y$ $+$ $54xy^2$

$(2) \,\,\,$ Simplify $27l^3$ $+$ $64m^3$ $+$ $108l^2m$ $+$ $144lm^2$

Now, let’s try to simplify the given algebraic expression.

$\,\,\,\,\,\,=\,\,\,$ $3^3 \times l^3$ $+$ $4^3 \times m^3$ $+$ $108l^2m$ $+$ $144lm^2$

$\,\,\,\,\,\,=\,\,\,$ $(3l)^3$ $+$ $(4m)^3$ $+$ $3 \times 36 \times l^2m$ $+$ $3 \times 48 \times lm^2$

$\,\,\,\,\,\,=\,\,\,$ $(3l)^3$ $+$ $(4m)^3$ $+$ $3lm(36l+48m)$

$\,\,\,\,\,\,=\,\,\,$ $(3l)^3$ $+$ $(4m)^3$ $+$ $3lm(3 \times 12l+3 \times 16m)$

$\,\,\,\,\,\,=\,\,\,$ $(3l)^3$ $+$ $(4m)^3$ $+$ $3lm \times 3 \times (12l+16m)$

$\,\,\,\,\,\,=\,\,\,$ $(3l)^3$ $+$ $(4m)^3$ $+$ $3lm \times 3 \times (4 \times 3l+4 \times 4m)$

$\,\,\,\,\,\,=\,\,\,$ $(3l)^3$ $+$ $(4m)^3$ $+$ $3lm \times 3 \times 4 \times (3l+4m)$

$\,\,\,\,\,\,=\,\,\,$ $(3l)^3$ $+$ $(4m)^3$ $+$ $3 \times 3l \times 4m \times (3l+4m)$

$\,\,\,\,\,\,=\,\,\,$ $(3l)^3$ $+$ $(4m)^3$ $+$ $3(3l)(4m)(3l+4m)$

Now, assume $a = 3l$ and $b = 4m$, and simplify the whole algebraic expression as a cube of sum of two terms.

$\implies$ $(3l)^3$ $+$ $(4m)^3$ $+$ $3(3l)(4m)(3l+4m)$ $\,=\,$ $(3l+4m)^3$

Proofs

The $a$ plus $b$ whole cube algebraic identity can be proved mathematically in the following two different methods.

Algebraic method

Learn how to derive the expansion of $a$ plus $b$ whole cube formula by the product of three sum basis binomials.

Geometric method

Learn how to prove the expansion of $a$ plus $b$ whole cube algebraic identity geometrically from the volume of a cube.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.