Find $x$ if $4 \ln x \,+\, 1 = 0$

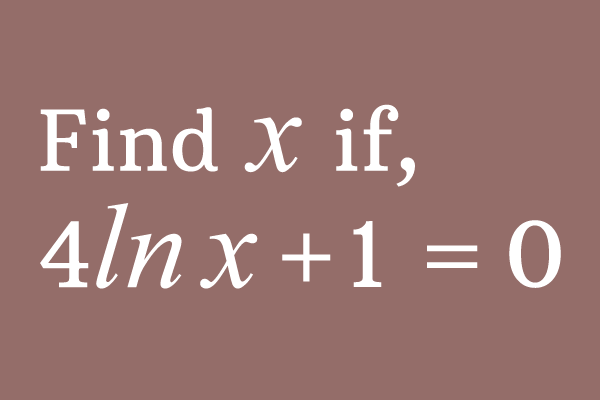
$4 \ln x \,+\, 1 = 0$ is a mathematical equation and $\ln x$ is natural logarithm which means $\log$ of $x$ to base $e$.

Move the number $1$ to right hand side.

$\implies 4 \ln x = -1$

The number $4$ is multiplying the $\ln x$ and it divides $-1$ if it is shifted to right hand side.

$$\implies \ln x = -\frac{1}{4}$$

According to natural logarithmic system, $\ln x = \log_{\displaystyle e} x$

$$\therefore \,\, \log_{\displaystyle e} x = -\frac{1}{4}$$

Now, it is time to consider the fundamental relation between logarithm and exponential notation.

$\log_{\displaystyle b} m = n \, \Leftrightarrow \, m = b^{\displaystyle n}$

Apply this rule to our expression to convert the logarithmic form into exponential notation.

$$\log_{\displaystyle e} x = -\frac{1}{4} \, \Leftrightarrow \, x = e^{\displaystyle – \Big(\dfrac{1}{4}\Big)}$$

$$\therefore \,\, x = e^{\displaystyle – \Big(\dfrac{1}{4}\Big)}$$

It can be expressed as follows.

$$\implies x = \frac{1}{e^{\displaystyle \Big(\dfrac{1}{4}\Big)}}$$

$$\therefore \,\, x = \frac{1}{\sqrt[\displaystyle 4]{e}}$$

The value of $x$ can also be expressed in another form.

We know that the value of $\dfrac{1}{4} = 0.25$. So, the answer can be expressed as follows.

$$\therefore \,\, x = e^{\displaystyle – 0.25}$$

The value of $x$ can be written in decimal form from this.

$$\therefore \,\, x \approx 0.7788$$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.