Properties of 0° Right triangle

There are three fundamental properties of a right triangle when its angle is zero degrees.

The length of opposite side is zero.
The lengths of adjacent side and hypotenuse are equal.
The angle of right angled triangle is zero and the other two angles are right angles.

Theorem

Geometrically, it is not possible to construct a zero degrees right triangle understandably but it can be imagined theoretically.

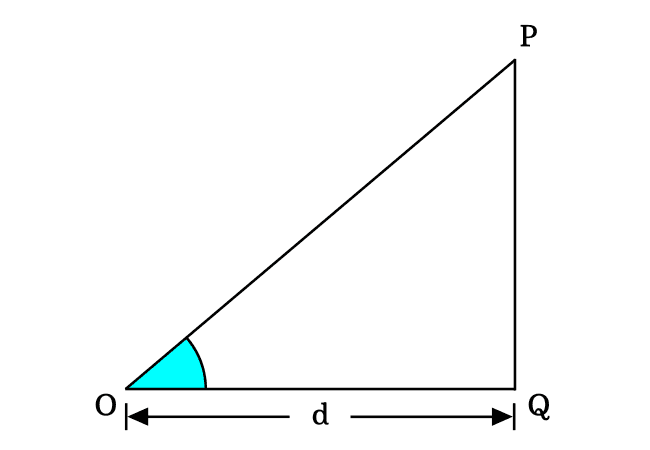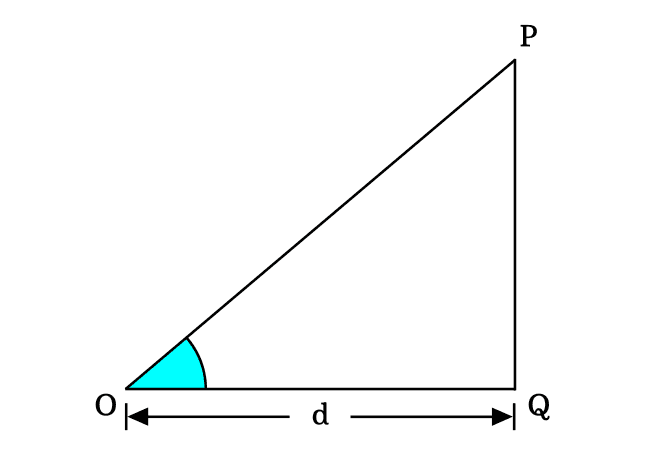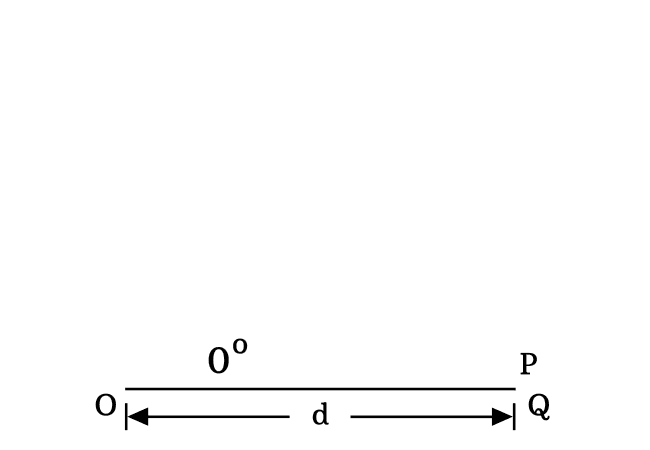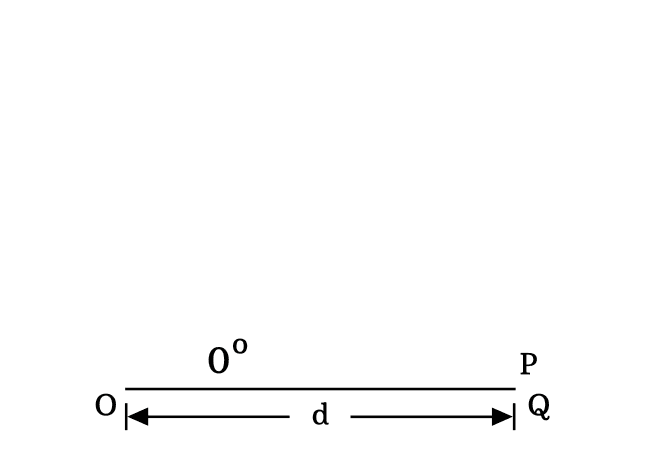
$\Delta POQ$ is a right triangle basically and the $\angle POQ$ represents the angle of this triangle. If the angle $POQ$ is equal to zero, then the triangle $POQ$ is called a zero degrees right angled triangle.

In this triangle, $\angle POQ$, $\angle OPQ$ and $\angle OQP$ are three angles but the $\angle POQ \,=\, 0^°$ and $\angle OQP \,=\, 90^°$

According to the angle sum property of a triangle, the sum of three interior angles in a triangle is $180^°$.

$\angle POQ + \angle OPQ + \angle OQP = 180^°$
$\implies 0^° + \angle OPQ + 90^° = 180^°$
$\implies \angle OPQ = 180^° – 90^°$
$\,\,\, \therefore \,\,\,\,\,\, \angle OPQ = 90^°$

Theoretically, it is proved that the two angles in a right angles are right angles when the angle of a right angled triangle is zero degrees.

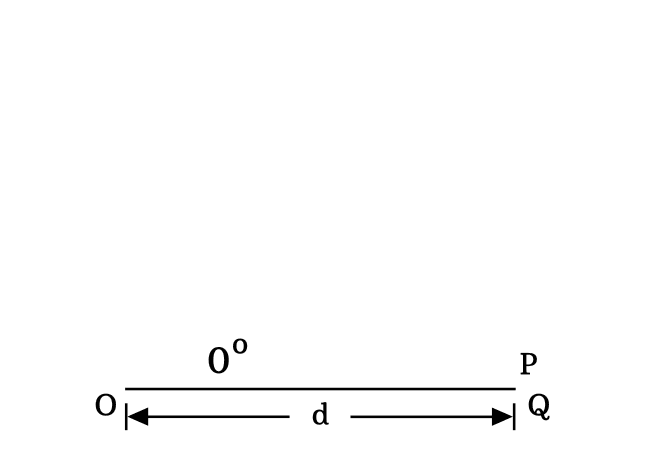
Assume that the length of adjacent side of this triangle is denoted by $d$.

The zero angle is possible geometrically in a right triangle when the length of opposite side is equal to zero.

$Length \, of \, Opposite \, side$ $\,=\,$ $0$

$\implies$ $PQ$ $\,=\,$ $0$

Due to zero length of opposite side, the length of hypotenuse is absolutely equal to the length of hypotenuse. So, remember this property when angle of right triangle is zero.

$\,\,\, \therefore \,\,\,\,\,\,$ $Length \, of \, Adjacent \, side$ $\,=\,$ $Length \, of \, Hypotenuse$ $\,=\,$ $d$

Proof

A right triangle is required to construct with zero angle for proving all its properties geometrically.

construction of right triangle whose angle equals to 0 degrees for its properties

Draw a horizontal line from point $\small P$ in a plane.
Identify zero angle from point $\small P$ and draw zero angle line from point $\small P$ but it appears on horizontal line.
Set compass to a length (for example $7 \, cm$) by a ruler. Now, draw an arc on zero angle line and they are intersected at point $\small Q$.
It’s not possible to draw a perpendicular line from point $\small Q$ to horizontal line because they both lie on same line. So, assume a perpendicular line is drawn from point $\small Q$ to horizontal line and it intersects the horizontal line at point $\small R$.

A right triangle ($\Delta RPQ$) is constructed with zero degrees angle. Now, it is time to study the properties of right angled triangle when its angle is zero.

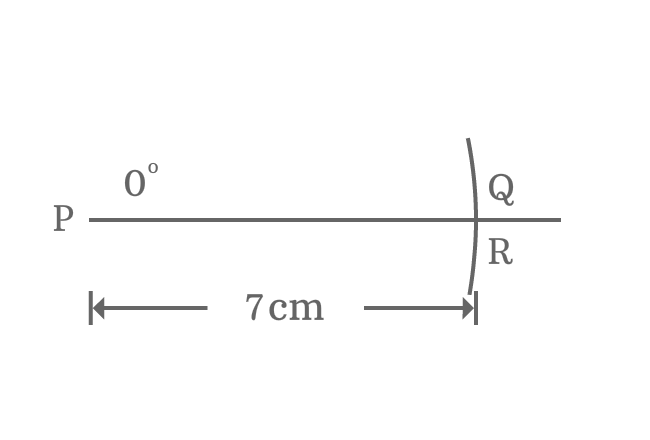
properties of right triangle whose angle equals to 0 degrees

$\small \overline{QR}$ is opposite side (or perpendicular). There is no distance between points $\small Q$ and $\small R$. So, the length of opposite side is zero.
$\small \overline{PQ}$ is hypotenuse. It is $7 \, cm$ in this case.
$\small \overline{PR}$ is adjacent side (or base). Due to zero length of opposite side, the length of adjacent side is equal to length of hypotenuse exactly. So, the length of adjacent side $\small \overline{PR}$ is also $7 \, cm$.

Therefore, it is proved that the length of opposite side is zero and the length of adjacent side is equal to length of hypotenuse when angle of right triangle is zero.

There is no angle between sides $\small \overline{PR}$ and $\small \overline{PQ}$. So, the angle of right triangle is zero. It means $\small \angle RPQ = 0^°$.
$\small \overline{QR}$ is a perpendicular line to side $\small \overline{PR}$ at point $\small R$. So, $\small \angle PRQ = 90^°$, which means second angle of right triangle is a right angle.
The length of perpendicular line ($\small \overline{QR}$) (known as opposite side) is zero. The hypotenuse and adjacent side are appeared in horizontal line position. Therefore, $\small \angle PQR = 90^°$. In other words, the third angle of right triangle is also a right angle.