y-intercept

The distance of an intersecting point of a straight line and vertical axis from origin is called $y$-intercept.

Introduction

A straight line often intersects vertical y-axis at a point. The distance from the intersecting point from origin in y-axis direction is known as $y$-intercept.

Example

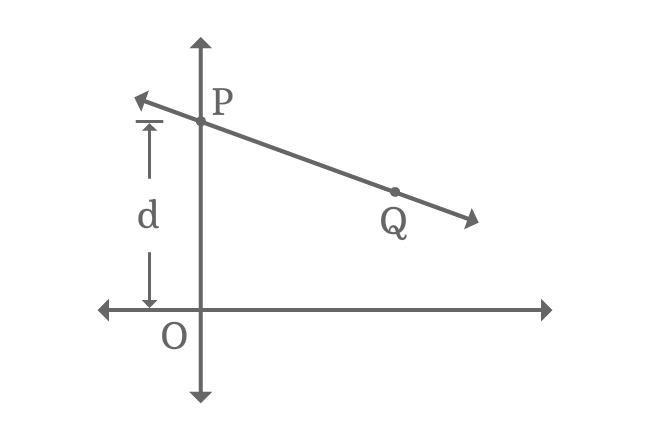
Consider a straight line in Cartesian coordinate system. It intersects the vertical $y$-axis at point $P$ and $Q$ is any point on the straight line.

The distance from origin to intersecting point of straight line $\overleftrightarrow{PQ}$ and $y$-axis in horizontal axis direction is $d$. The distance $d$ is called as $y$-intercept.

$y$-intercept $\,=\,$ $d$

$\implies OP$ $\,=\,$ $d$

The intersecting point $P$ is on $y$-axis. So, its $x$-coordinate is equal to zero but its $y$-coordinate equals to $y$-intercept. Therefore, the intersecting point $P$ in the form of coordinates is $(0, d)$.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.