Proof of $(x+a)(x+b)$ formula in Geometric Method

Formula

${(x+a)}{(x+b)}$ $\,=\,$ $x^2+(a+b)x+ab$

Proof

The $(x+a)(x+b)$ algebraic identity can be derived geometrically by the concept of areas of rectangle and square.

Calculating Area of Rectangle

1. Take a rectangle. Divide it as two parts horizontally and the lengths of them are $x$ and $a$.
2. Now, divide the same rectangle vertically but the length of one part should be $x$ and take the length of remaining part is $b$.
3. The length and width of whole rectangle are $x+a$ and $x+b$ respectively. Therefore, the area of the rectangle is ${(x+a)} \times {(x+b)}$ geometrically.

Calculating Areas of Geometrical Shapes

The geometrical approach splits a rectangle as a square and three different small rectangles. Now, calculate area of every geometric shape mathematically.

1. The length of side of square is $x$. So, the area of square is $x^2$
2. Length and width of first rectangle are $b$ and $x$ respectively. So, area of the rectangle is $bx$.
3. Length and width of second rectangle are $x$ and $a$ respectively. So, area of this rectangle is $xa$.
4. Length and width of third rectangle are $b$ and $a$ respectively. So, area of this rectangle is $ba$.

Calculating Areas of Geometrical Shapes

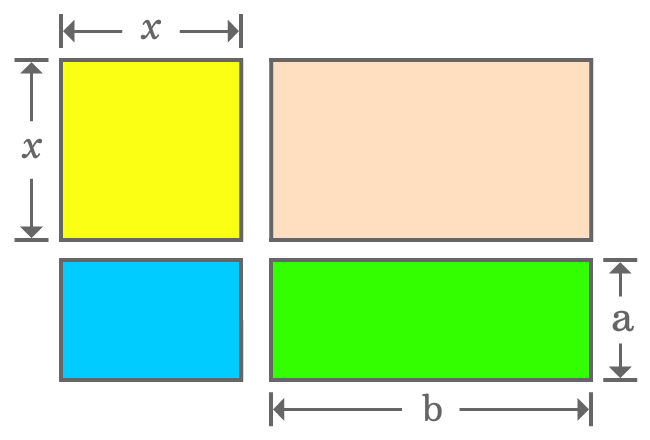
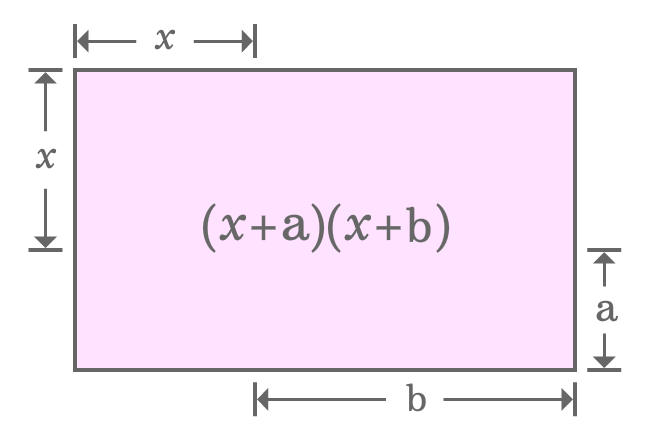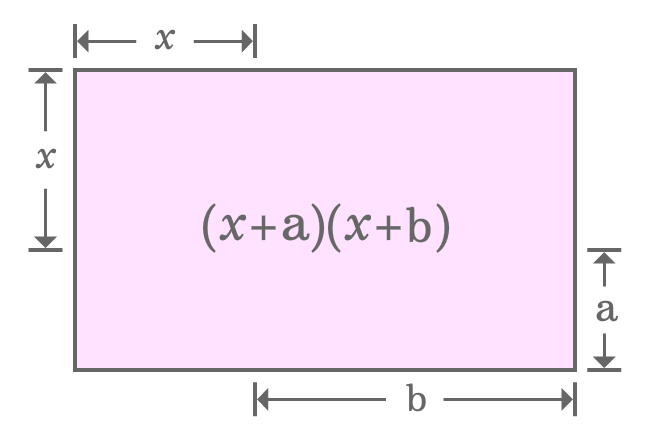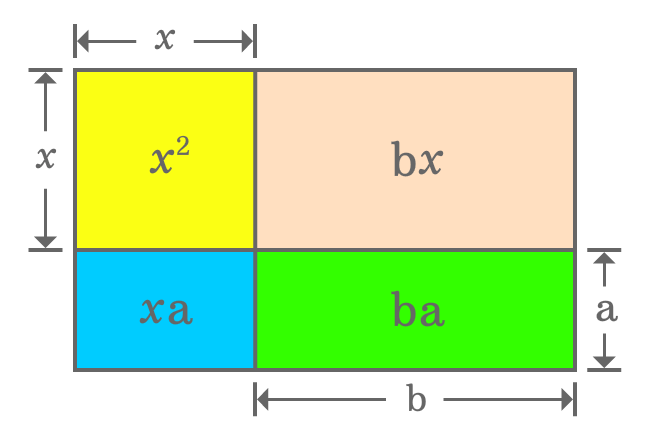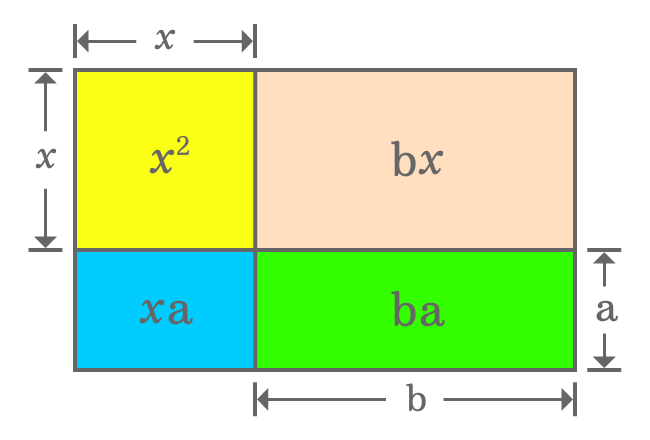
It is derived that the area of a whole rectangle is ${(x+a)}{(x+b)}$. Actually, the same rectangle is divided as a square and three small different rectangles. So, the area of rectangle should be equal to the sum of the areas of one square and three different rectangles.

${(x+a)}{(x+b)}$ $\,=\,$ $x^2+bx+xa+ba$

$\implies$ ${(x+a)}{(x+b)}$ $\,=\,$ $x^2+bx+ax+ab$

$\implies$ ${(x+a)}{(x+b)}$ $\,=\,$ $x^2+ax+bx+ab$

$\,\,\, \therefore \,\,\,\,\,\,$ ${(x+a)}{(x+b)}$ $\,=\,$ $x^2+(a+b)x+ab$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.