Vertices of a Quadrilateral

A point where any two edges of a quadrilateral meet, is called a vertex of a quadrilateral.

Introduction

A quadrilateral is expressed graphically by connecting the endpoints of four line segments as a closed geometric shape. The endpoints of the four line segments are intersected at four different locations and each intersecting point of every two line segments of a quadrilateral is called a vertex of a quadrilateral. So, a quadrilateral has four vertices possibly.

Example

$□ \, CDEF$ is a quadrilateral and it is formed by four line segments.

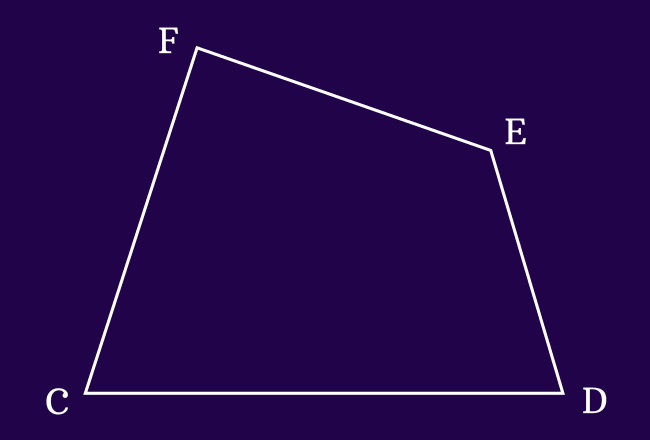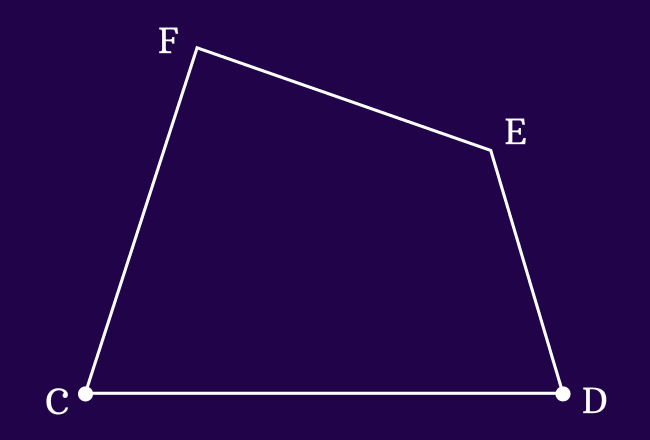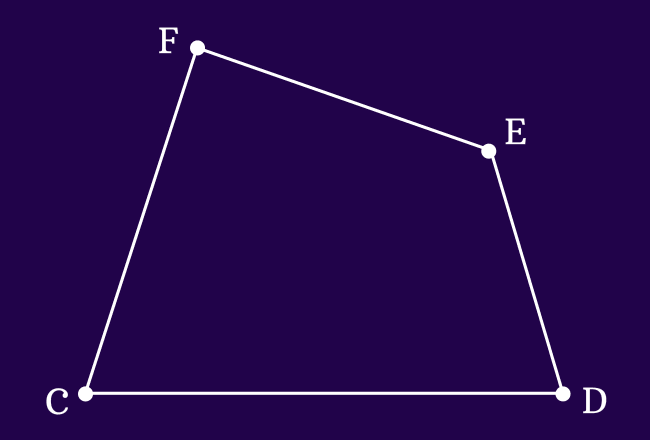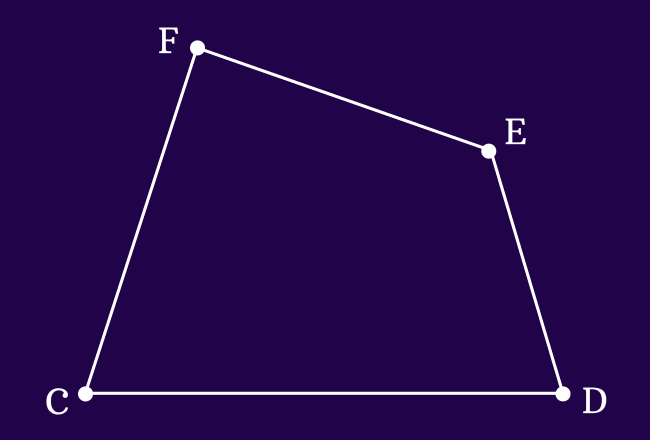
1. The edges $\small \overline{CD}$ and $\small \overline{DE}$ are intersected at point $\small D$. So, the point $\small D$ is called as a vertex.
2. The sides $\small \overline{DE}$ and $\small \overline{EF}$ are intersected at point $\small E$. So, the point $\small E$ is called as a vertex.
3. The sides $\small \overline{EF}$ and $\small \overline{FC}$ are intersected at point $\small F$. So, the point $\small F$ is called as a vertex.
4. The sides $\small \overline{FC}$ and $\small \overline{CD}$ are intersected at point $\small C$. So, the point $\small C$ is called as a vertex.

Therefore, the intersecting points $C,$ $D,$ $E$ and $F$ are called the vertices of the quadrilateral $CDEF$.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.