Variable

A literal that represents a changeable quantity is called a variable.

Introduction

According to English Language, the meaning of the word “variable” is changeable. The mathematics is all about the numbers. So, the variables are used to represent the changeable quantities and they are denoted by literals.

Usage

The variables are used in two cases.

It is mainly used to represent a changeable quantity.
It is also used to denote the unknown quantity.

Examples

Let’s learn both cases to understand how the variables are used in algebraic mathematics.

Changeable quantity

A variable is used to denote the changeable quantity.

Take, the letter $t$ is used to represent the total number of apples falls on the ground. Initially, there is no apple on the floor. Hence, it is denoted by $t = 0$ algebraically.

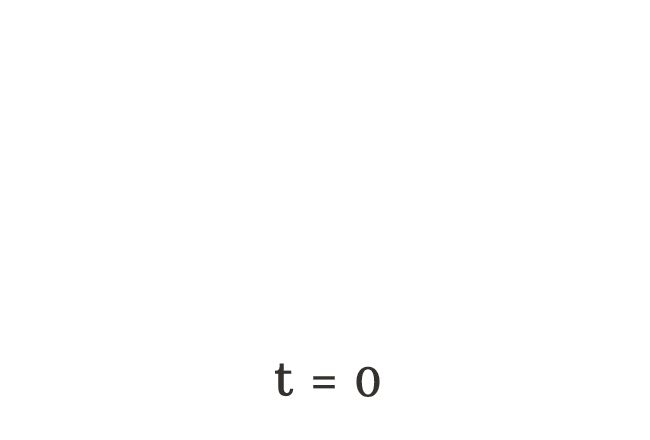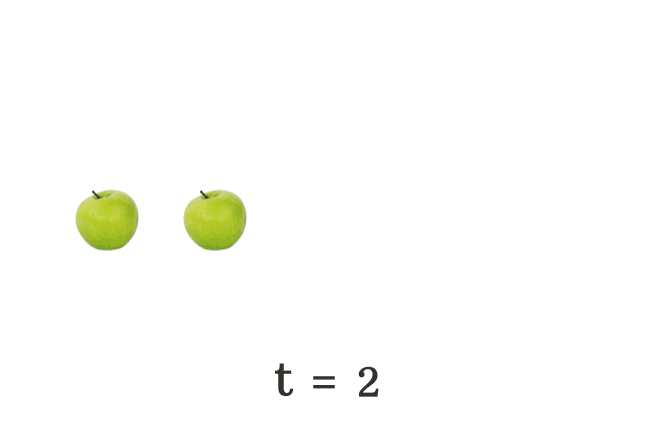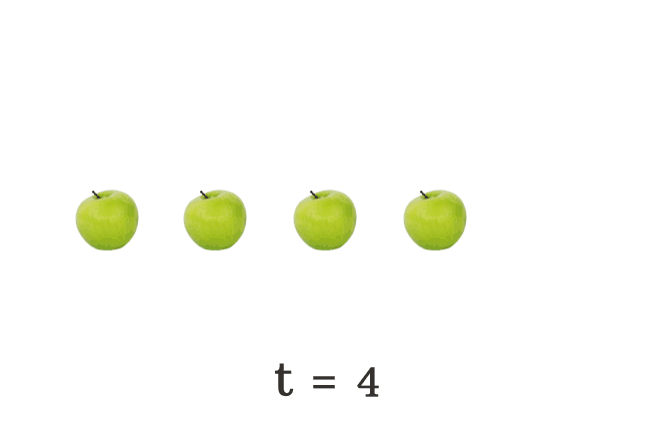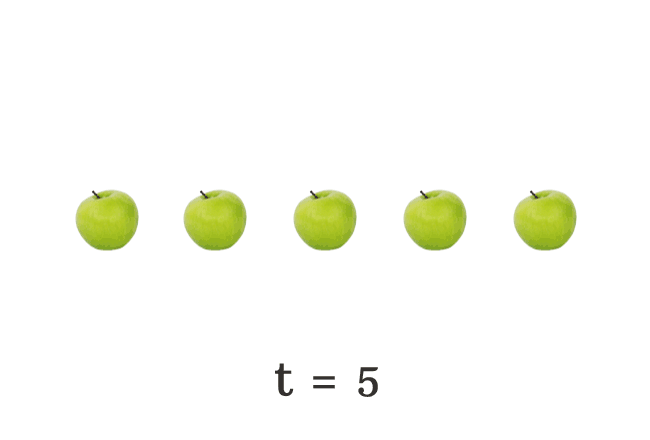
$(1) \,\,\,\,\,\,$ $t \,=\, 0$

$(2) \,\,\,\,\,\,$ $t \,=\, 1$

$(3) \,\,\,\,\,\,$ $t \,=\, 2$

$(4) \,\,\,\,\,\,$ $t \,=\, 3$

$(5) \,\,\,\,\,\,$ $t \,=\, 4$

$(6) \,\,\,\,\,\,$ $t \,=\, 5$

The total number of apples falls on the floor is changing every time. Hence, the literal $t$ is called a variable.

Unknown quantity

A variable is also used to represent an unknown quantity.

There are some apples in a box but we don’t know exactly how many apples they are. Hence, the quantity is denoted by a literal. For example, $m$.

Can you guess how many apples they are?

You guess a number and I guess a number. It is changed for every person. So, an unknown quantity is considered as a changeable quantity. Therefore, a literal number that represents an unknown quantity is usually called as a variable. In this case, $m$ is a variable.