A term that represents a ratio of lengths of opposite side to adjacent side at an angle of a right triangle is called the tangent.
Tangent is a name, used to represent the quotient of lengths of opposite side by adjacent side at an angle of a right triangle. It’s simply written in its short form as $\tan$ in mathematics.
The quotient (or) ratio between lengths of opposite and adjacent sides, returns a value and it is called tangent value of simply tan value.
$\dfrac{Length \, of \, Opposite \, side}{Length \, of \, Adjacent \, side}$
The tan value is actually calculated by the ratio. So, the tangent is often called as a trigonometric ratio generally.
Every tan value is calculated at an angle of a right triangle. So, the tangent of an angle is expressed mathematically by writing tangent in its short form with angle of the triangle.
For example, if $x$ is an angle of right triangle, then the tangent of angle is written as $\tan{x}$. It is read as tan of angle $x$. The $\tan{x}$ is a function mathematically. Therefore, a tan function is usually called as a trigonometric function.
Thus, the tan functions ($\tan{A}$, $\tan{\alpha}$, and so on) are defined in trigonometry.
$\Delta CAB$ is a right triangle and its angle is theta ($\theta$).
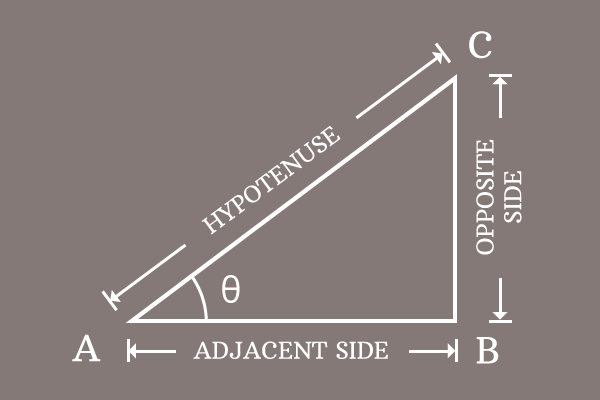
Tangent of angle is written as $\tan{\theta}$ in this case.
$\tan{\theta} \,=\, \dfrac{Length \, of \, Opposite \, side}{Length \, of \, Adjacent \, side}$
It is used as a formula to calculate the value of tangent at any angle of the right triangle.
$BC$ is length of opposite side (perpendicular) and $AB$ is length of adjacent side (base) in this example.
$\,\,\, \therefore \,\,\,\,\,\, \tan{\theta} \,=\, \dfrac{BC}{AB}$
The list of exact values of tangent functions in fraction and decimal forms in a table with proofs.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved