Perimeter of a triangle

The sum of lengths of all three sides of a triangle is called perimeter of a triangle.

Introduction

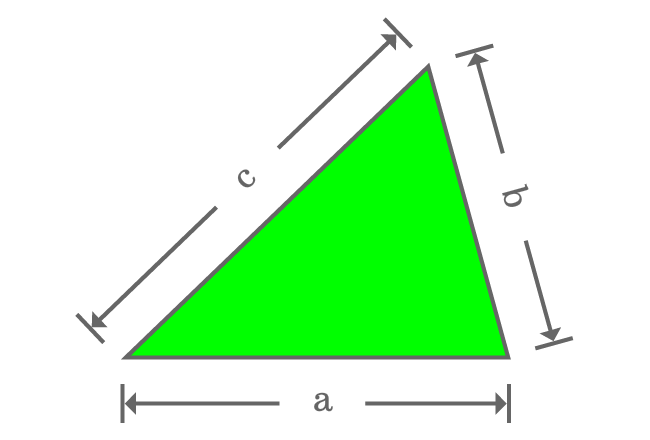
The boundary of a triangle is the perimeter of the triangle but its boundary is geometrically formed by the intersection of three line segments. Therefore, the perimeter of triangle is the total of the lengths of three sides of the triangle.

Formula

If $a$, $b$ and $c$ are lengths of sides of a triangle, then the perimeter of the triangle is equal to sum of them.

$P_{t} \,=\, a+b+c$

Note, the letter $P_{t}$ is used in the formula to represent the perimeter of the triangle.

Example

$\Delta TRS$ is a triangle and we have to find the perimeter of this triangle.

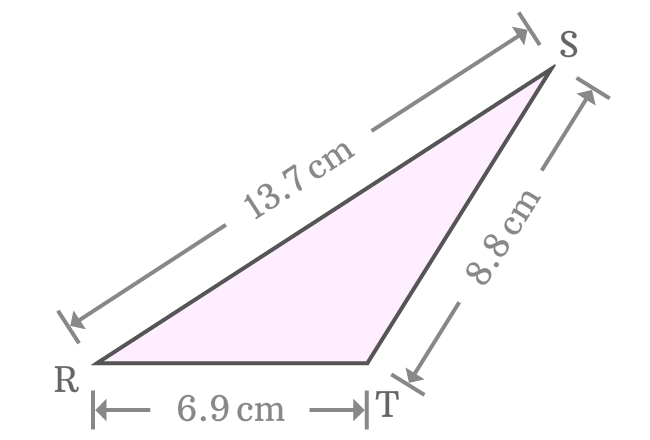
The length of each side of this triangle is given as follows

1. The length of side ($\small \overline{RT}$) is equal to $6.9 \, cm$
2. The length of side ($\small \overline{RS}$) is equal to $13.7 \, cm$
3. The length of side ($\small \overline{ST}$) is equal to $8.8 \, cm$

Now, it is time to find the perimeter for the given lengths of the triangle.

$P_{t} \,=\, RT+RS+ST$

$\implies P_{t} \,=\, 6.9+13.7+8.8$

$\,\,\, \therefore \,\,\,\,\,\, P_{t} \,=\, 29.4$

Therefore, it is calculated that the perimeter of the $\Delta TRS$ is $29.4 \, cm$. You can calculate the perimeter of any triangle in this way.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.