Properties of Right triangle when angle equals to 90°

Properties

There are three fundamental properties between sides of a right triangle when its angle equals to $90$ degrees.

1. The length of adjacent side is zero.
2. The lengths of opposite side and hypotenuse are equal.
3. Two angles are right angles and an angle is zero angle.

Theorem

$\Delta QPR$ is a triangle, which represents a right triangle with $90^°$ angle.

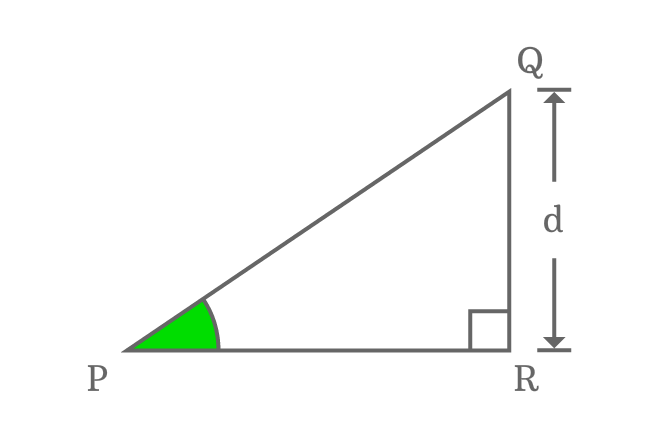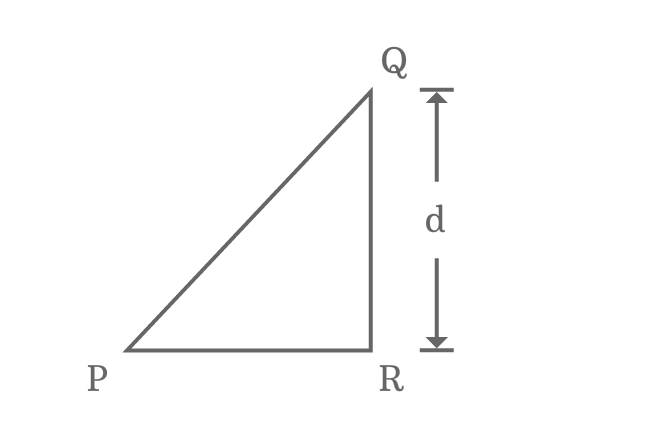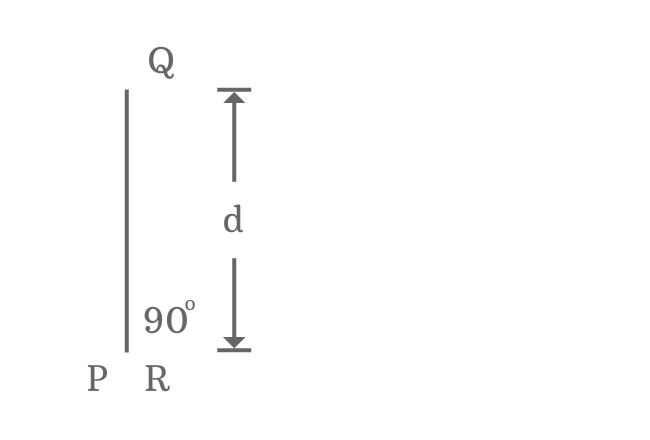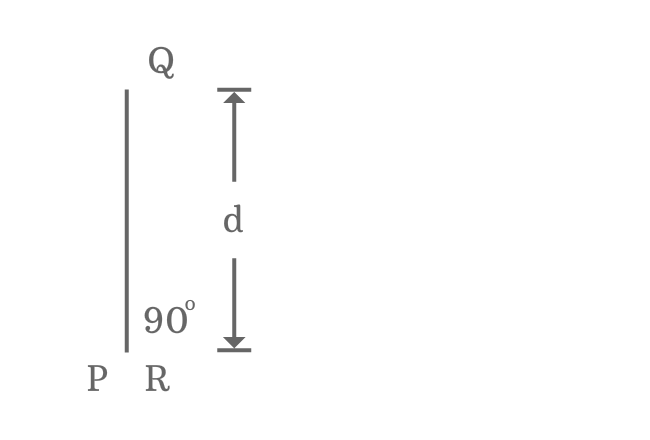
It is possible to construct a right triangle with $90^°$ angle only when the length of adjacent side (base) is zero.

$Length \, of \, Adjacent \, side$ $\,=\,$ $0$

$\implies PR \,=\, 0$

When length of adjacent side ($\overline{PR}$) is zero, the lengths of opposite side (perpendicular) and hypotenuse are equal.

In this example, the length of opposite side is represented by $d$.

$\,\,\, \therefore \,\,\,\,\,\,$ $Length \, of \, Opposite \, side$ $\,=\,$ $Length \, of \, Hypotenuse$ $\,=\,$ $d$

$\implies QR = PQ = d$

Now, let’s talk about the angles of this triangle.

The length of adjacent side becomes zero because the $\angle PQR$ becomes zero angle. Therefore $\angle PQR = 0^°$. Whenever the $\angle PQR$ becomes zero, the angles $\angle RPQ$ and $\angle QRP$ become right angles.

$\angle RPQ$ $\,=\,$ $\angle QRP$ $\,=\,$ $90^°$

Proof

The properties of right triangle when its angle equals to $\dfrac{π}{2}$, can be proved geometrically by constructing a right triangle with $90$ degrees angle.

1. Mark a point $L$ on plane and then draw a horizontal line.
2. Make centre of protractor to coincide with point $L$ and also coincide its right side base line with the horizontal line. Now, identify $90^°$ on protractor and mark on plane at that point.
3. Draw a line from point $L$ through the $90$ degrees angle point.
4. Take compass and adjust it to any length. In this example, it is set to $8 \, cm$ with the reference of a ruler. Later, draw an arc on the $90$ degrees line from point $L$ and it cuts the line at point $M$.
5. From point $M$, draw a perpendicular line to horizontal line and take it intersects the horizontal line at point $N$. In this case, $90$ degrees line and horizontal line both are appeared one on one and the points $L$ and $N$ both are same due to no distance between them.

A right triangle, represented by $\Delta NLM$ is formed geometrically. Finally, it is your time to study the properties of right triangle when its angle is a right angle.

$\overline{LN}$ is adjacent side and its length is zero because there is no distance between the points $L$ and $N$.

$LN \,=\, 0$

$\overline{MN}$ represents opposite side and $\overline{LM}$ represents hypotenuse but the points $L$ and $N$ are at same position. Therefore, the lengths of opposite side and hypotenuse are equal if the angle of right triangle is $90^°$. In $\Delta NLM$, the length of hypotenuse is $8 \, cm$. Hence, the length of opposite side is also equal to $8 \, cm$.

$LM \,=\, MN \,=\, 8$

Due to zero length of adjacent side, the $\angle LMN = 0^°$. The $\angle MLN$ and $\angle MNL$ are right angles. Therefore, $\angle MLN = \angle MNL = 90^°$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.