Right hand limit
The value of a function as its input approaches some value with negligible increment is called the right-hand limit, and also called as the right sided limit.
Introduction
Let’s take, $x$ is a variable, a function is defined in terms of $x$ and it is simply written as $f(x)$ in mathematics. Assume, $a$ represents a constant but the slight increment in $a$ is denoted by $a^+$ and $L$ represents the limit of the function $f(x)$.
Now, the right sided limit of the function $f(x)$ is $L$ as the variable $x$ approaches $a$ with negligibly slight increment. In this case, $a^+$ is the closer value of $a$ from right side in Cartesian coordinate system. It is written in the following mathematical form in calculus.
$L \,=\, \displaystyle \large \lim_{x \,\to\, a^+}{\normalsize f(x)}$
Remember, the representation $x \,\to\, a^-$ means it is neither $a$ nor $+a$ but slightly greater than $a$ and very closer to $a$.
Example
The concept of right-sided limit can be understood from the below example.
Evaluate $\displaystyle \large \lim_{x \,\to\, 1^+}{\normalsize (x-2)^3}$
In this problem, we have to calculate the value of the function $(x-2)^3$ as the input $x$ closer to $1$ from right-side in the Cartesian coordinate system. As per the two-dimensional space, $2$ and $3$ are near points from right-side of point $1$. Therefore, let us calculate the values of the given function for them.
- $f(2) = (2-2)^3 = 0$
- $f(3) = (3-2)^3 = 1$
In fact, the point $x = 2$ is one unit away from the point $x = 1$ in right-side. Similarly, the point $x = 3$ is two units away from the point $x = 1$ in right-side. The two points are near points but not closer from right-side of the point $x = 1$.
But, the point $x = 1.1$ is closer point to point $x = 1$ than $x = 2$ and $x = 3$. So, calculate the value of the function.
$f(1.1) = (1.1-2)^3 = -0.729$
There is no doubt about it that the point $x = 1.1$ is closer to point $x = 1$ but the point $x = 1.1$ is $0.1$ unit away from point $x = 1$ and the difference between them is small but not negligible. So, the value of the function $(x-2)^3$ at point $x = 1.1$ cannot be considered as the limit of the function as $x$ approaches $1$ from right side.
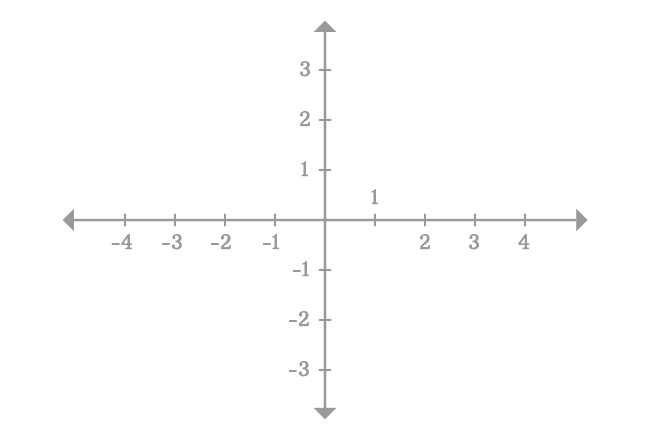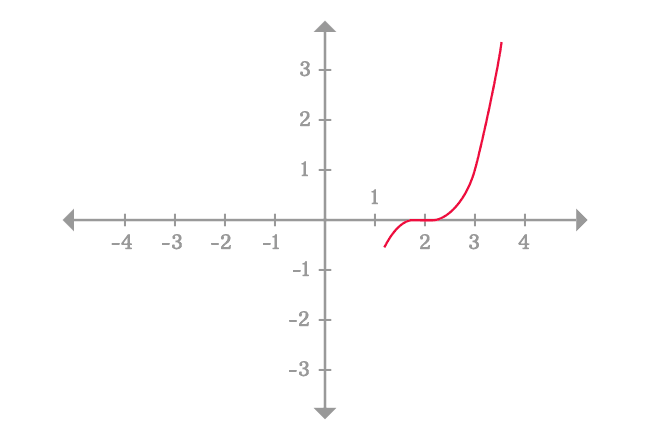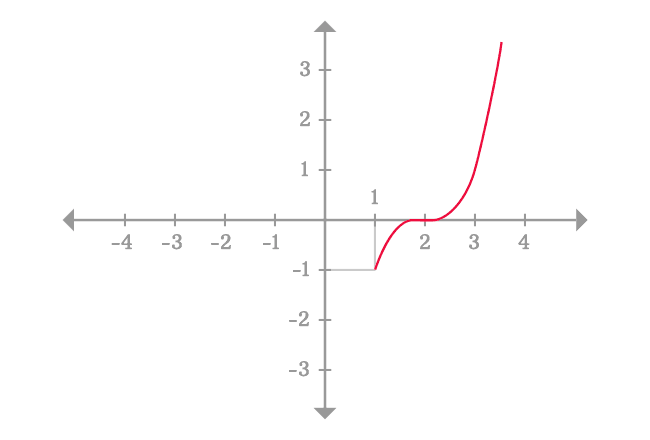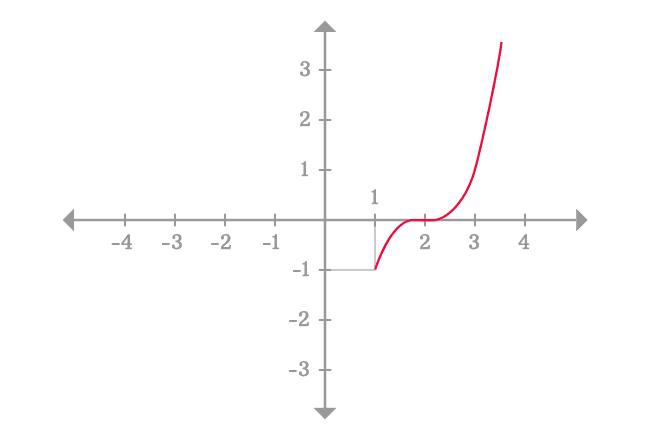
Therefore, we should have to take the points, which are very closer to the point $x = 1$ from right-side, for example $x = 1.01$ $,$ $1.001$ $,$ $1.0001$ and so on.
- $f(1.01)$ $=$ $(1.01-2)^3$ $=$ $-0.970299$
- $f(1.001)$ $=$ $(1.001-2)^3$ $=$ $-0.997002999$
- $f(1.0001)$ $=$ $(1.0001-2)^3$ $=$ $-0.999700029999$
- $f(1.00001)$ $=$ $(1.00001-2)^3$ $=$ $-0.999970000299999$
For $x = 1.01$ $,$ $1.001$ $,$ $1.0001$ and $1.00001$, the values of the function are $-0.970299$, $-0.997002999$, $-0.999700029999$ and $-0.999970000299999$ respectively.
Actually, $1.01$ $\ne$ $1.001$ $\ne$ $1.0001$ $\ne$ $1.00001$ but $1.01 \approx 1$ $,$ $1.001 \approx 1$ $,$ $1.0001 \approx 1$ and $1.00001 \approx 1$. Similarly, $-0.970299$ $\ne$ $-0.997002999$ $\ne$ $-0.999700029999$ $\ne$ $-0.999970000299999$ but $-0.970299 \approx -1$ $\,$ $-0.997002999 \approx -1$ $,$ $-0.999700029999 \approx -1$ and $-0.999970000299999 \approx -1$.
It can be understand much better from the following tabular form.
| $\Large x$ | $f(x)$ | ||
|---|---|---|---|
| $Actual$ | $Approximate$ | $Actual$ | $Approximate$ |
| $3$ | $3$ | $0$ | $0$ |
| $2$ | $2$ | $1$ | $1$ |
| $1.1$ | $1.1$ | $−0.729$ | $−0.729$ |
| $1.01$ | $1$ | $−0.970299$ | $-1$ |
| $1.001$ | $1$ | $−0.997002999$ | $-1$ |
| $1.0001$ | $1$ | $−0.999700029999$ | $-1$ |
| $1.00001$ | $1$ | $−0.999970000299999$ | $-1$ |
| $\vdots$ | $\vdots$ | $\vdots$ | $\vdots$ |
| $1$ | $1$ | $-1$ | $-1$ |
The values of the given function are not equal but their values are approximately same and it is equal to $-1$ because the value of $x$ is very closer to $1$. So, you can consider any closer value of $x$ as $x$ approaches $1$ from right hand side for evaluating the limit.
For example, Consider $x = 1.00526$. It is a number, which can be reached from $1$ with slight increment and the difference between them is negligible small.
$1.00526-1 = 0.00526 \approx 0$
Therefore, the limit of a function $(x-2)^3$ as $x$ approaches $1$ can be calculated by taking the value of $x$ with slight increment.
$\displaystyle \large \lim_{x \,\to\, 1^+}{\normalsize (x-2)^3}$ $\,=\,$ $(1.00526-2)^3$
$\implies$ $\displaystyle \large \lim_{x \,\to\, 1^+}{\normalsize (x-2)^3}$ $\,=\,$ $(-0.99474)^3$
$\implies$ $\displaystyle \large \lim_{x \,\to\, 1^+}{\normalsize (x-2)^3}$ $\,=\,$ $-0.984302857268424$
$\,\,\, \therefore \,\,\,\,\,\,$ $\displaystyle \large \lim_{x \,\to\, 1^+}{\normalsize (x-2)^3}$ $\,\approx\,$ $-1$
Therefore, the limit of the function $(x-2)^3$ as $x$ approaches $1$ with slight increment is equal to $-1$ and it is called the right-hand limit or right-sided limit.
Remember, $x \,\to\, 1^+$ means $x \ne 1$ and $x \ne +1$ but $x > 1$ and $x \approx 1$ in this case.
