Multiplicative inverse

Math Doubts

When the product of two quantities equals to one, one quantity is called a multiplicative inverse (or reciprocal) of another quantity.

Introduction

The quantities are often involved in multiplication in mathematics. In a special case, the product of two quantities is equal to one. It is possible when a quantity is in opposite form in another quantity.

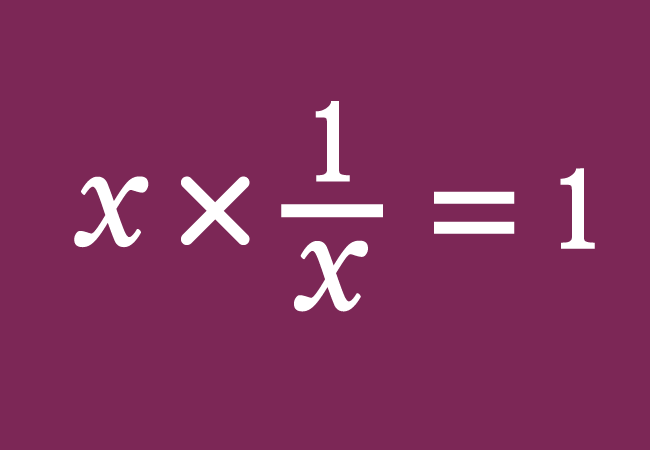
In some cases, the meaning of opposite is expressed by a word “inverse” in mathematics.
The product of two quantities equals to one is actually calculated by the multiplication.

According to these two considerable factors, one quantity is called a multiplicative inverse of the remaining quantity.

For example, $6$ and $\dfrac{1}{6}$ are two quantities and multiply them to get their product.

$6 \times \dfrac{1}{6}$

$=\,\,\,$ $\dfrac{6}{1} \times \dfrac{1}{6}$

$=\,\,\,$ $\dfrac{6 \times 1}{1 \times 6}$

$=\,\,\,$ $\dfrac{6}{6}$

$=\,\,\,$ $\dfrac{\cancel{6}}{\cancel{6}}$

$=\,\,\,$ $1$

Therefore, it is cleared that the product of a quantity and quotient of one by the same quantity is equal to one.

$\therefore\,\,\,$ $6 \times \dfrac{1}{6}$ $\,=\,$ $1$

Therefore, the number $\dfrac{1}{6}$ is called the multiplicative inverse or reciprocal of the number $6$ and vice-versa.

Algebraic form

Let $x$ be a variable and it represents a quantity. The second quantity is unknown. So, it can be denoted by a variable $y$. Assume that the product of both variables is equal to one.

$x \times y \,=\, 1$

Now, we can evaluate the variable $y$ in terms of $x$.

$\implies$ $y \,=\, \dfrac{1}{x}$

Therefore, the variable $y$ is equal to the quotient of one by $x$.

$(1).\,\,\,$ $\dfrac{1}{x}$ is called the multiplicative inverse of $x$.

$(2).\,\,\,$ $x$ is called the reciprocal of the $\dfrac{1}{x}$

Remember that, $\dfrac{1}{x}$ is simply written as $x^{-1}$ in mathematics.