Lower Unitriangular matrix
Fact-checked:
Definition
A square matrix in which all the elements above the leading diagonal are zero and all the entries on the main diagonal are one, is called a lower unitriangular matrix.
Introduction
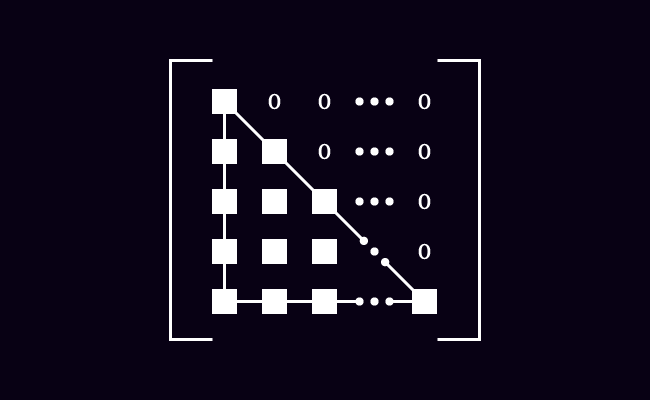
Let’s understand the meanings of the words “lower” and “triangular” firstly before learning the concept of the lower triangular matrix and its internal structure.
- The word “Lower” means situated below another part.
- The word “Triangular” means shaped like a triangle.
The entries above the main diagonal are zero in a square matrix in a special case. The elements on the leading diagonal and the entries below the primary diagonal form a triangle shape. Therefore, the square matrix is called a lower triangular matrix.
$L \,=\,
\begin{bmatrix}
e_{11} & 0 & 0 & \cdots & 0\\
e_{21} & e_{22} & 0 & \cdots & 0\\
e_{31} & e_{32} & e_{33} & \cdots & 0\\
\vdots & \vdots & \vdots & \ddots & \vdots\\
e_{n1} & e_{n2} & e_{n3} & \cdots & e_{nn}
\end{bmatrix}$
Basically, the matrix $L$ is a square matrix of order $n$. The elements $e_{11}$, $e_{22}$, $e_{33}$, $e_{44}$ $\cdots$ $e_{nn}$ are the entries on the major diagonal. The elements on the leading diagonal and the entries below the principal diagonal form a triangle shape but the elements above the primary diagonal are zeros. Hence, the matrix $L$ is called a lower triangular matrix.
Condition
$L \,=\,
{\begin{bmatrix}
e_{\displaystyle ij}
\end{bmatrix}}_{\displaystyle n \times n}$
There is a mathematical condition in the case of a lower triangular matrix. The entries are zero if $i < j$ and they are elements above the leading diagonal of the matrix. The remaining entries are non-zeros and form a triangle shape.
It means $e_{ij} = 0$, if $i < j$.
Examples
Observe the below three matrices to know the concept of lower triangular matrix.
$A \,=\,
\begin{bmatrix}
1 & 0\\
6 & -5
\end{bmatrix}$
The matrix $A$ is a second order square matrix.
- The elements $1$ and $-5$ are entries on the major diagonal.
- The entry below the main diagonal is $6$ but the entry above the principal diagonal is $0$.
- The entries on the main diagonal $1$ and $-5$, and the entry below the primary diagonal $6$ form a triangle shape.
Hence, the matrix $A$ is called a lower triangular matrix.
$B \,=\,
\begin{bmatrix}
9 & 0 & 0\\
4 & 1 & 0\\
7 & 2 & -3
\end{bmatrix}$
The matrix $B$ is a third order square matrix.
- The entries $9$, $1$ and $-3$ are elements on the principal diagonal.
- The elements below the leading diagonal are $4$, $7$ and $2$ but the entries above the primary diagonal are $0$.
- The diagonal entries $9$, $1$ and $-3$, and the elements below the main diagonal form a triangle shape.
So, the matrix $B$ is called a lower triangular matrix.
$C =
\begin{bmatrix}
5 & 0 & 0 & 0\\
-1 & 6 & 0 & 0\\
8 & 3 & 9 & 0\\
-2 & -6 & -7 & 2\\
\end{bmatrix}$
The matrix $C$ is a fourth order square matrix.
- The entries $5$, $6$ and $9$ and $2$ are diagonal elements on the main diagonal.
- The elements below the primary diagonal are $-1$, $8$, $3$, $-2$, $-6$ and $-7$ but the entries above the major diagonal are $0$.
- The diagonal elements and the entries below the leading diagonal form a triangle shape.
Therefore, the matrix $C$ is called a lower triangular matrix.

