Lower Triangular matrix

Definition

A square matrix in which all the entries above the main diagonal are zero, is called a lower triangular matrix.

Introduction

Let’s understand the meanings of the words “lower” and “triangular” firstly before learning the concept of the lower triangular matrix and its internal structure.

The word “Lower” means situated below another part.
The word “Triangular” means shaped like a triangle.

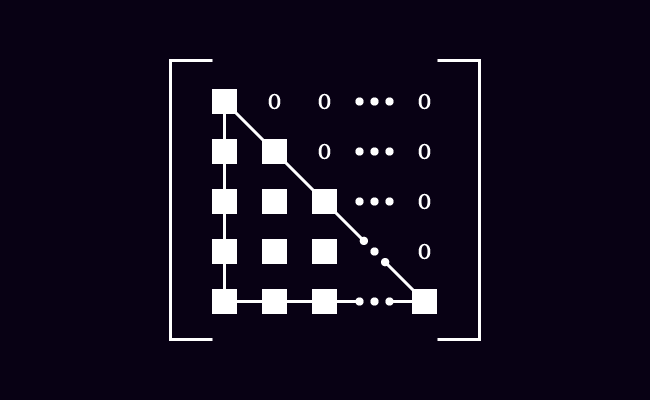
The entries above the main diagonal are zero in a square matrix in a special case. The elements on the leading diagonal and the entries below the primary diagonal form a triangle shape. Therefore, the square matrix is called a lower triangular matrix.

$L \,=\, \begin{bmatrix} e_{11} & 0 & 0 & \cdots & 0\\ e_{21} & e_{22} & 0 & \cdots & 0\\ e_{31} & e_{32} & e_{33} & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ e_{n1} & e_{n2} & e_{n3} & \cdots & e_{nn} \end{bmatrix}$

Basically, the matrix $L$ is a square matrix of order $n$. The elements $e_{11}$, $e_{22}$, $e_{33}$, $e_{44}$ $\cdots$ $e_{nn}$ are the entries on the major diagonal. The elements on the leading diagonal and the entries below the principal diagonal form a triangle shape but the elements above the primary diagonal are zeros. Hence, the matrix $L$ is called a lower triangular matrix.

Condition

$L \,=\, {\begin{bmatrix} e_{\displaystyle ij} \end{bmatrix}}_{\displaystyle n \times n}$

There is a mathematical condition in the case of a lower triangular matrix. The entries are zero if $i < j$ and they are elements above the leading diagonal of the matrix. The remaining entries are non-zeros and form a triangle shape.

It means $e_{ij} = 0$, if $i < j$.

Examples

Observe the below three matrices to know the concept of lower triangular matrix.

$A \,=\, \begin{bmatrix} 1 & 0\\ 6 & -5 \end{bmatrix}$

The matrix $A$ is a second order square matrix.

The elements $1$ and $-5$ are entries on the major diagonal.
The entry below the main diagonal is $6$ but the entry above the principal diagonal is $0$.
The entries on the main diagonal $1$ and $-5$, and the entry below the primary diagonal $6$ form a triangle shape.

Hence, the matrix $A$ is called a lower triangular matrix.

$B \,=\, \begin{bmatrix} 9 & 0 & 0\\ 4 & 1 & 0\\ 7 & 2 & -3 \end{bmatrix}$

The matrix $B$ is a third order square matrix.

The entries $9$, $1$ and $-3$ are elements on the principal diagonal.
The elements below the leading diagonal are $4$, $7$ and $2$ but the entries above the primary diagonal are $0$.
The diagonal entries $9$, $1$ and $-3$, and the elements below the main diagonal form a triangle shape.

So, the matrix $B$ is called a lower triangular matrix.

$C = \begin{bmatrix} 5 & 0 & 0 & 0\\ -1 & 6 & 0 & 0\\ 8 & 3 & 9 & 0\\ -2 & -6 & -7 & 2\\ \end{bmatrix}$

The matrix $C$ is a fourth order square matrix.

The entries $5$, $6$ and $9$ and $2$ are diagonal elements on the main diagonal.
The elements below the primary diagonal are $-1$, $8$, $3$, $-2$, $-6$ and $-7$ but the entries above the major diagonal are $0$.
The diagonal elements and the entries below the leading diagonal form a triangle shape.

Therefore, the matrix $C$ is called a lower triangular matrix.