Equation of a straight line when line passes through origin with slope

Equation

$y \,=\, mx$

It is an equation of a straight line when a straight line passes through origin with some slope in two dimensional Cartesian coordinate system.

Proof

A straight line is passing through origin $(O)$ of the Bi-dimensional Cartesian coordinate system and $P$ is any point on the straight line. The straight line is represented by $\overleftrightarrow{OP}$ in geometry.

Geometric construction of a right triangle

1. $O(0, 0)$ and $P(x, y)$ are points on the straight line in coordinate form in the two dimensional space.
2. Assume, the angle made by the straight line with $x$-axis is theta and its slope is denoted by $m$.
3. Draw a perpendicular line to $x$ axis from point $P$ and it intersects the horizontal axis at point $Q$ perpendicularly. Thus, it formed a right triangle, denoted by $\Delta QOP$ in geometric system.

Express slope of line in coordinate form

The slope of the straight line is $m$ and it is equal to the tan of angle theta.

$m \,=\, \tan{\theta}$

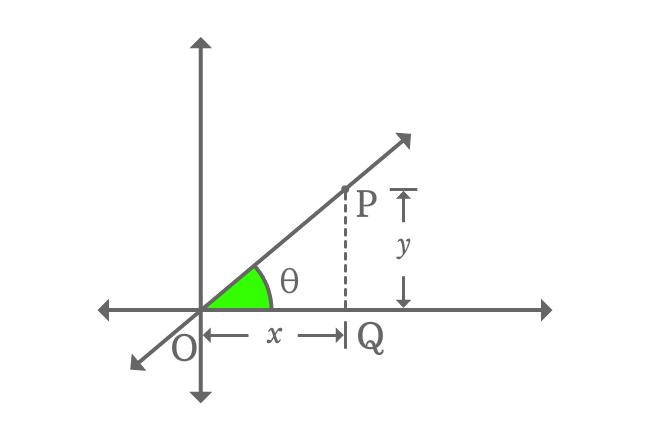
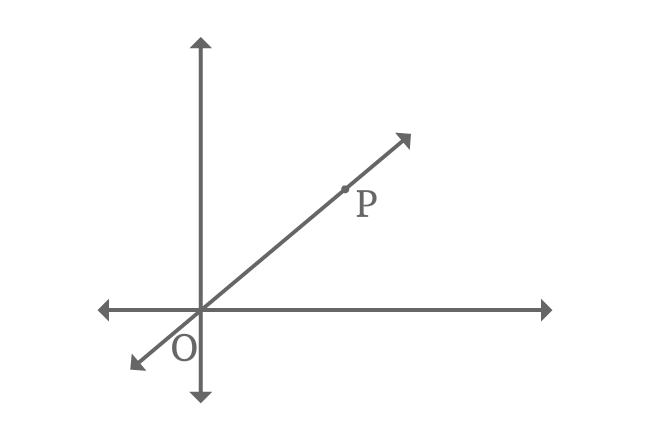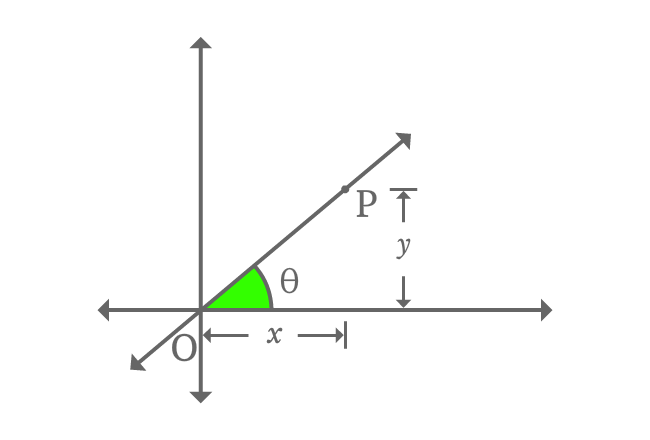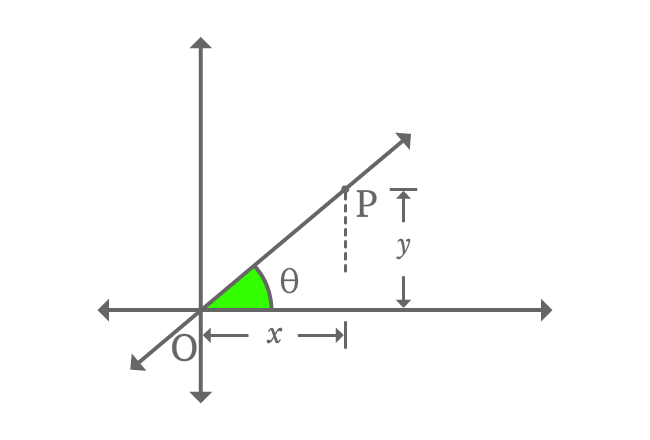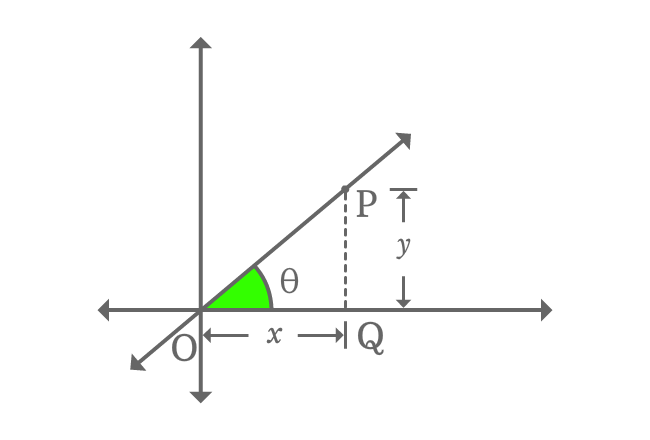
Now, find the value of $\tan{\theta}$ in terms of coordinates of right triangle $QOP$.

$\tan{\theta} \,=\, \dfrac{PQ}{OQ}$

$\implies \tan{\theta} \,=\, \dfrac{y}{x}$

Geometrically, tan of angle theta is equal to slope of straight line $m$.

$\,\,\, \therefore \,\,\,\,\,\, m \,=\, \dfrac{y}{x}$

Equation of a Line in Mathematical form

The equation of a straight line when a straight line passes through origin with some slope can be written in algebraic form from the mathematical relation of slope of line with coordinates of any point on that straight line.

$\,\,\, \therefore \,\,\,\,\,\, y \,=\, mx$

It is similar to the slope intercept form of a straight line. It can be derived from slope intercept form linear equation by placing zero as $x$ or $y$ intercept of the line.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.