Math Doubts

Inverse sine function

Definition

The inverse of the sine function is called the inverse sine function.

The sine function represents a value of the ratio of the length of opposite side to length of hypotenuse at the respective angle of a triangle, whereas the inverse sine function represents an angle for a value of the ratio of the length of opposite side to length of the hypotenuse of the same triangle.

Function

The inverse sine is written in short form as $\large \arcsin$ or $\large \sin^{-1}$ in mathematics.

According to the definition of the inverse sine function, the inverse sine function is expressed in mathematical form as follows.

$\large \sin^{-1} \normalsize \Bigg[\dfrac{Length \, of \, Opposite \, side}{Length \, of \, Hypotenuse}\Bigg]$ $\,=\,$ $Angle \, of \, the \, Triangle$

It can also be written in the following form.

$\large \arcsin \normalsize \Bigg[\dfrac{Length \, of \, Opposite \, side}{Length \, of \, Hypotenuse}\Bigg]$ $\,=\,$ $Angle \, of \, the \, Triangle$

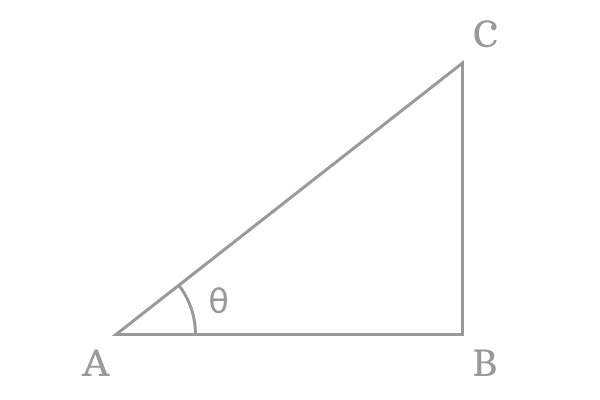
right angled triangle

For example, $\Delta BAC$ is a right angled triangle and its angle is $\theta$. $\overline{BC}$ and $\overline{AC}$ are opposite side and hypotenuse, and their lengths are $BC$ and $AC$ respectively.

The arc sine is expressed in mathematical form as follows for the $\Delta BAC$.

$\large \sin^{-1} \normalsize \Big(\dfrac{BC}{AC}\Big) \,=\, \theta \,\,\,$ or $\,\,\, \large \arcsin \normalsize \Big(\dfrac{BC}{AC}\Big) \,=\, \theta$

Assume, the quotient of the length of the opposite side by the length of hypotenuse is $x$.

Then, $\large \sin^{-1} x \,=\, \theta \,\,\,$ or $\,\,\, \large \arcsin x \,=\, \theta$

The $\sin^{-1} x$ or $\arcsin x$ is the representation of the inverse sine function in mathematical form.

Example

The functionality of the arcsine or inverse sine function can be understood geometrically from this example.

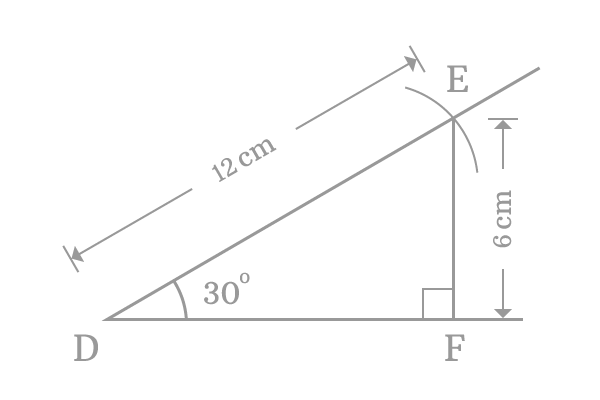
right angled triangle with 30 degrees angle
  1. Draw a horizontal line by using a ruler and $D$ is the left side endpoint of the line.
  2. Take Protector, and draw a line of $30^\circ$ angle from point $D$.
  3. Use compass and set the distance between needle point to pencil point to $12$ centimetre with the help of a ruler and then draw an arc on $30$ degrees angle line from point $D$. The intersecting point of arc and $30^\circ$ line is called point $E$.
  4. Use set square, and draw a perpendicular line to horizontal line from point $E$. The line perpendicularly intersected the horizontal line at point $F$.

The geometric procedure is constructed a right angled triangle $DEF$ and its angle is $30^\circ$. Now, measure, the length of the opposite side $\overline{EF}$ by using a ruler. You will observe that it is $6 \, cm$ exactly.

The functionality of the inverse sine function is expressed in mathematically in the following way.

$\sin^{-1} \Big(\dfrac{6}{12}\Big) \,=\, 30^\circ$

$\implies$ $\require{cancel} \sin^{-1} \Big(\dfrac{\cancel{6}}{\cancel{12}}\Big) \,=\, 30^\circ$

$\therefore \,\,\,\,\,\,$ $\sin^{-1} (0.5) \,=\, 30^\circ$

It can also be expressed in another form.

$\therefore \,\,\,\,\,\,$ $\arcsin (0.5) \,=\, 30^\circ$

The inverse of the sine function is given that the angle of the right angled triangle is $30^\circ$ for the value $0.5$.