Intersecting lines

A straight line that divides another straight line at a point by passing is called an intersecting line.

Introduction

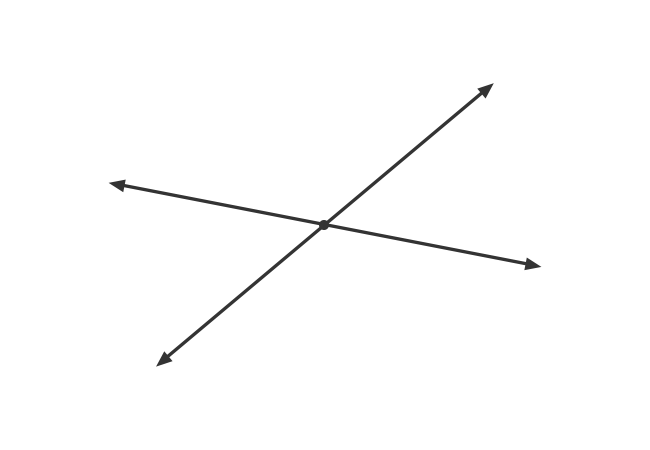
In English language, the word “intersect” means divide something by passing.

The travelling of one straight line definitely divides another straight line at a point for continuing its journey when two straight lines are non-parallel.

Due to their internal division at a point, one straight line is called an interesting line to the other straight line. Therefore, the two straight lines are called the intersecting lines.

Examples

Look at the following two cases to learn the concept of intersecting lines with understandable examples.

Direct Intersection

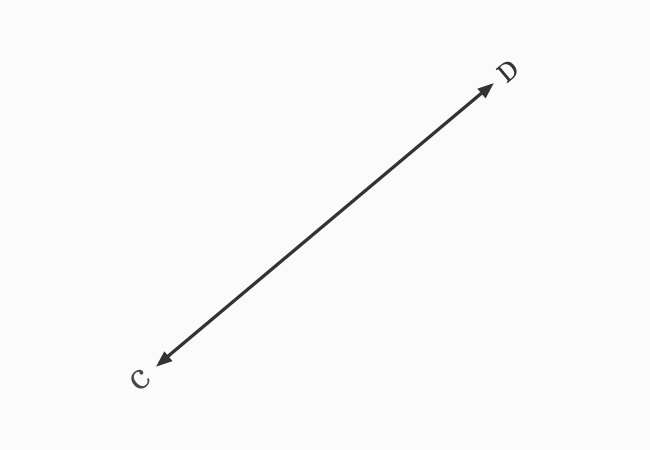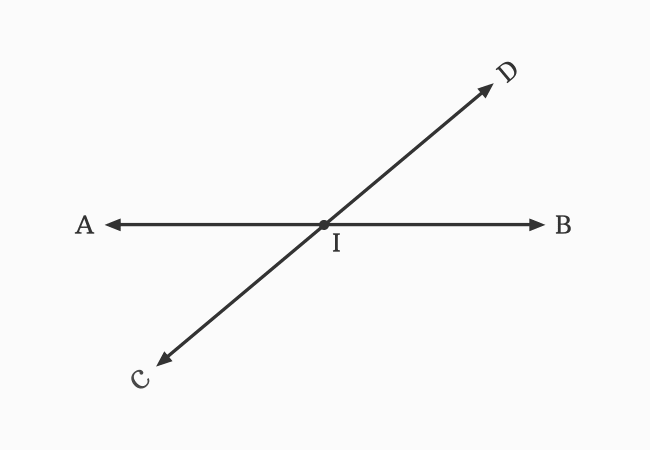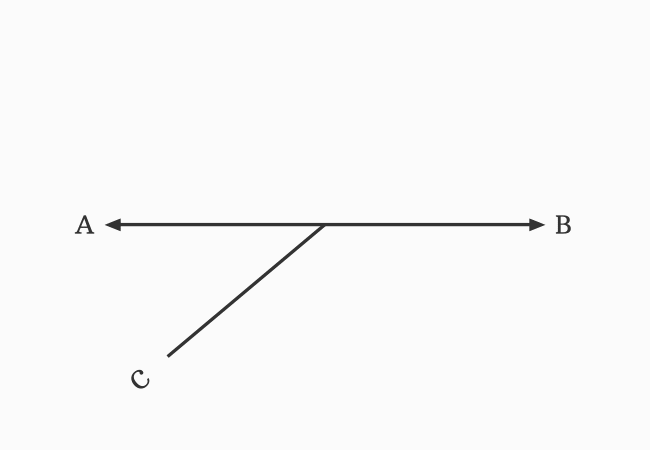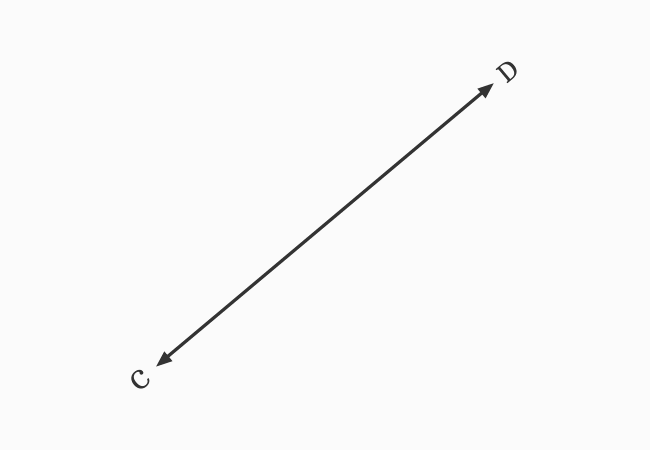
$\small \overleftrightarrow{AB}$ and $\small \overleftrightarrow{CD}$ are two straight lines, and they both meet each other at a point $I$ during their travelling. It seems, the straight line $\small \overleftrightarrow{AB}$ divides another straight line $\small \overleftrightarrow{CD}$ at point $I$, and vice-versa.

The straight line $\small \overleftrightarrow{AB}$ is called an intersecting line of $\small \overleftrightarrow{CD}$ and the straight line $\small \overleftrightarrow{CD}$ is called an intersecting line of $\small \overleftrightarrow{AB}$. Hence, the straight lines $\small \overleftrightarrow{AB}$ and $\small \overleftrightarrow{CD}$ are called the intersecting lines.

Extension for Intersection

The non-parallel lines cannot maintain equal distance between them at their corresponding opposite points. Therefore, the non-parallel lines always intersect in a plane at a point and they are called the intersecting lines.

$\small \overleftrightarrow{PQ}$ and $\small \overleftrightarrow{RS}$ are two straight lines in a plane. It seems they do not meet each other at a point.

The picture shows that the straight lines $\small \overleftrightarrow{PQ}$ and $\small \overleftrightarrow{RS}$ are not parallel lines. So, they should meet each other at a point in a plane when they are extended until they meet each other.

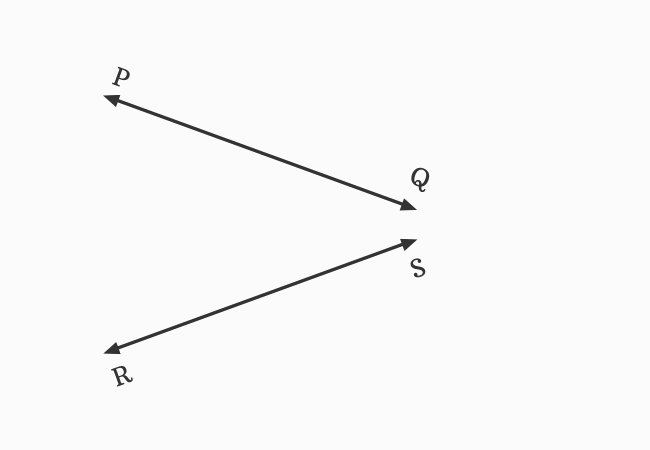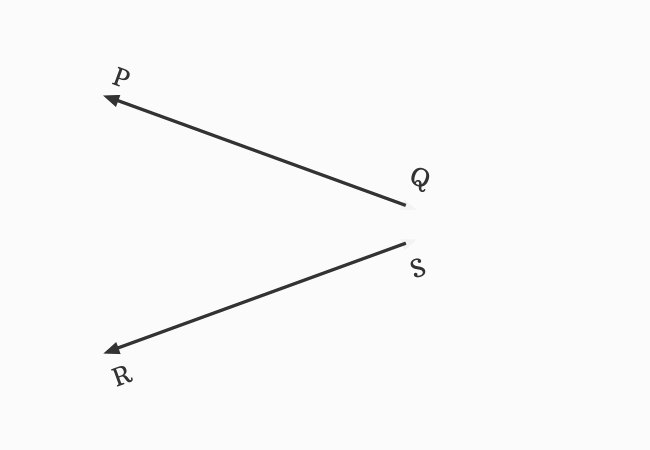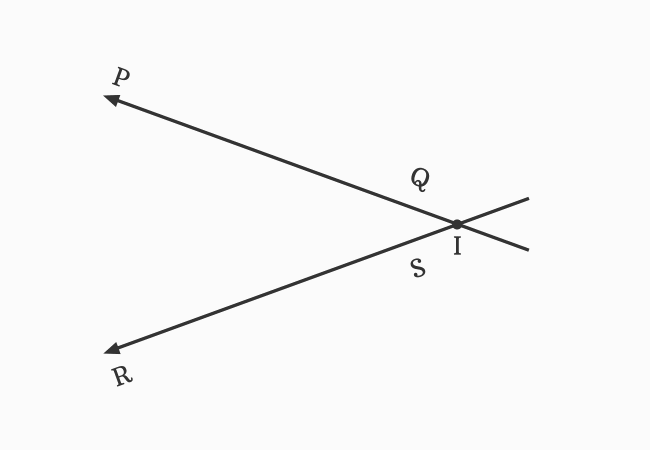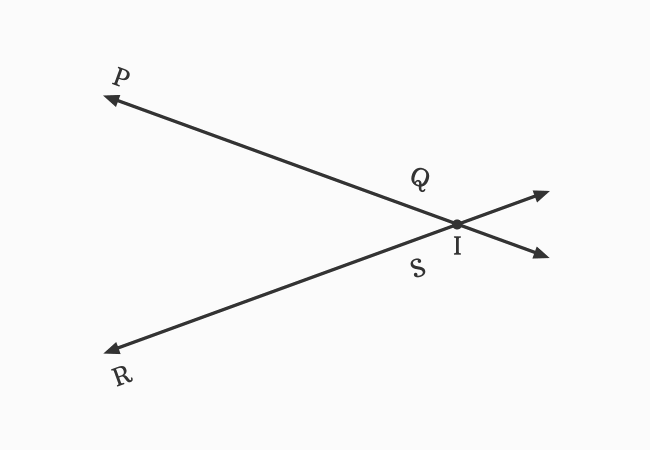
Now, the straight lines $\small \overleftrightarrow{PQ}$ and $\small \overleftrightarrow{RS}$ are met at point $I$ to continue their journey. Hence, they are also called the intersecting lines.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.