There are three fundamental properties of a right triangle when its angle is zero degrees.
Geometrically, it is not possible to construct a zero degrees right triangle understandably but it can be imagined theoretically.
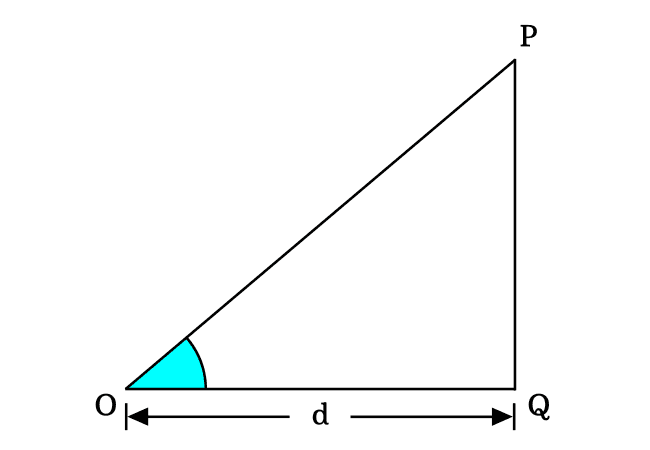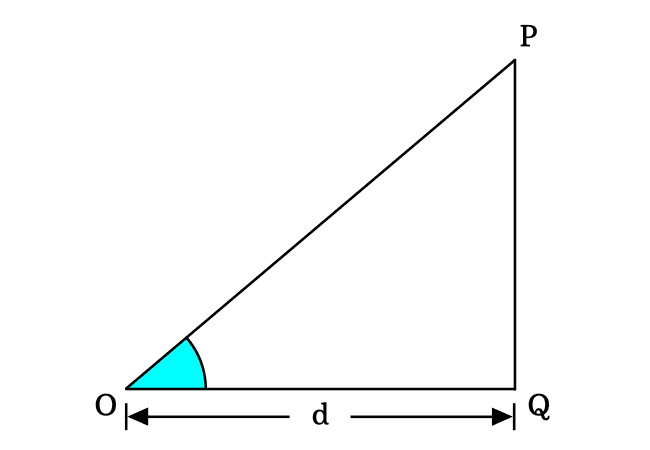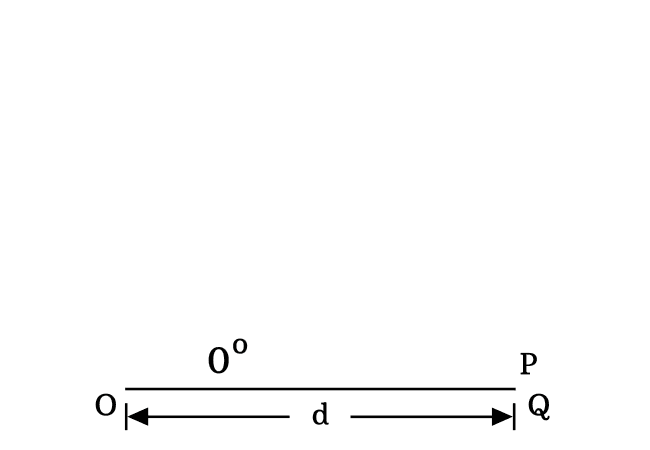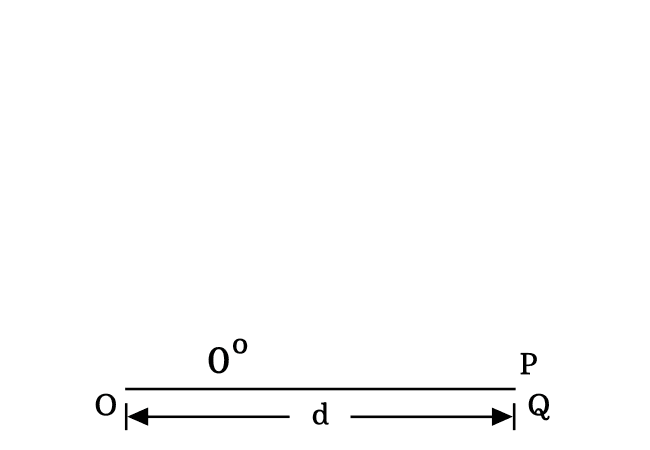
$\Delta POQ$ is a right triangle basically and the $\angle POQ$ represents the angle of this triangle. If the angle $POQ$ is equal to zero, then the triangle $POQ$ is called a zero degrees right angled triangle.
In this triangle, $\angle POQ$, $\angle OPQ$ and $\angle OQP$ are three angles but the $\angle POQ \,=\, 0^°$ and $\angle OQP \,=\, 90^°$
According to the angle sum property of a triangle, the sum of three interior angles in a triangle is $180^°$.
$\angle POQ + \angle OPQ + \angle OQP = 180^°$
$\implies 0^° + \angle OPQ + 90^° = 180^°$
$\implies \angle OPQ = 180^° – 90^°$
$\,\,\, \therefore \,\,\,\,\,\, \angle OPQ = 90^°$
Theoretically, it is proved that the two angles in a right angles are right angles when the angle of a right angled triangle is zero degrees.
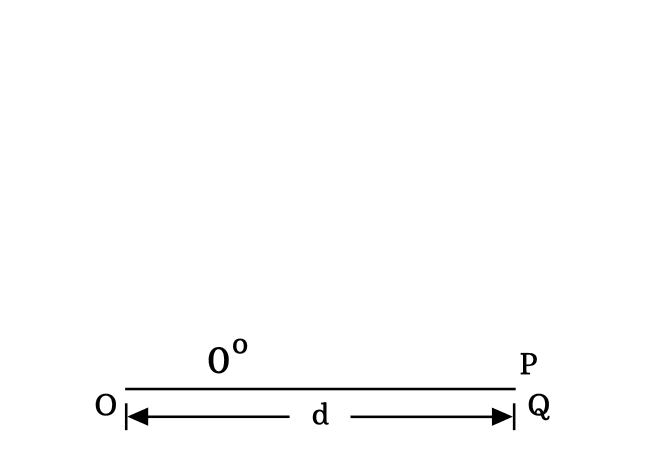
Assume that the length of adjacent side of this triangle is denoted by $d$.
The zero angle is possible geometrically in a right triangle when the length of opposite side is equal to zero.
$Length \, of \, Opposite \, side$ $\,=\,$ $0$
$\implies$ $PQ$ $\,=\,$ $0$
Due to zero length of opposite side, the length of hypotenuse is absolutely equal to the length of hypotenuse. So, remember this property when angle of right triangle is zero.
$\,\,\, \therefore \,\,\,\,\,\,$ $Length \, of \, Adjacent \, side$ $\,=\,$ $Length \, of \, Hypotenuse$ $\,=\,$ $d$
A right triangle is required to construct with zero angle for proving all its properties geometrically.

A right triangle ($\Delta RPQ$) is constructed with zero degrees angle. Now, it is time to study the properties of right angled triangle when its angle is zero.
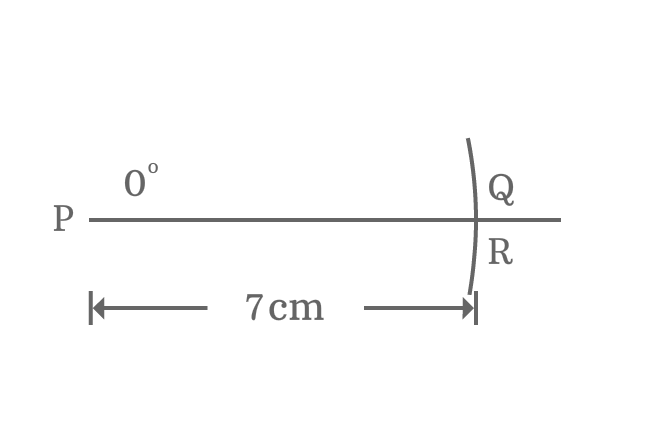
Therefore, it is proved that the length of opposite side is zero and the length of adjacent side is equal to length of hypotenuse when angle of right triangle is zero.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved