A part of the circumference of a circle is called an arc.

The circumference of a circle can be divided as two parts by cutting it at two different points. Each part of the circumference of the circle is called as an arc.
The arcs are classified into two types on the basis of lengths of the arcs of the circle.
Imagine a circle and divide it at two points $I$ and $J$. It separates the circumference of the circle as two parts.

If length of the arc is minor, then it is called as minor arc.
If length of the arc is major, then it is called as major arc.
$I$ and $J$ are endpoints for the both minor and major arcs. It confuses everyone if both arcs are expressed in mathematics by their endpoints. Hence, a point on each arc is considered additionally to represent each arc clearly in mathematics.
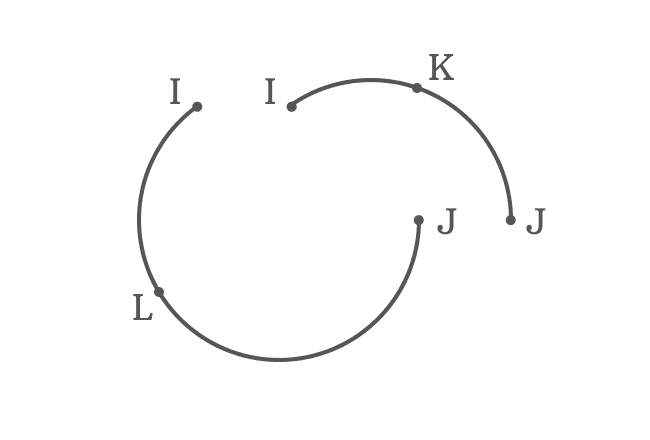
The name of the point on the arc is written between its end points and also arc symbol ($\large ⌢$) is displayed additionally over three of them to tell that an arc is formed by them.
$K$ and $L$ are any points on minor and major arcs respectively. The symbol ($\large ⌢$) is used to represent an arc in mathematics.
The minor arc of a circle is called as $arc \, IKJ$ and it is denoted by $\stackrel{\Huge ⌢}{IKJ}$ in mathematics. Similarly, the major arc of a circle is called as $arc \, ILJ$ and it is expressed in mathematics as $\stackrel{\Huge ⌢}{ILJ}$.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved