Geometrical interpretation of the Definite integrals

The explanation of the definite integral by a mathematical equation definitely confuses everyone at beginner level but the geometrical interpretation does not create any problem to anyone. So, it is always recommended for everyone to understand the concept of definite integration by the geometrical system.

Construction

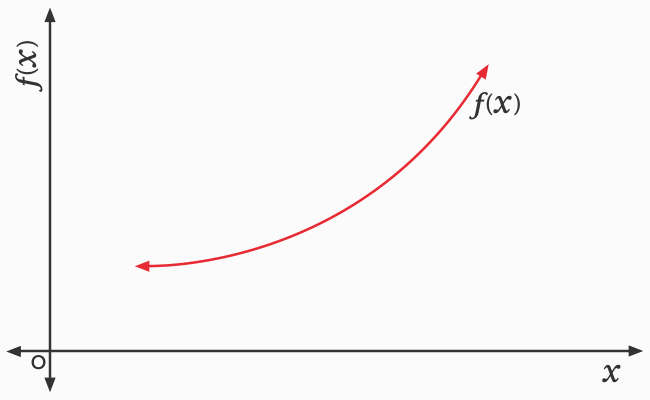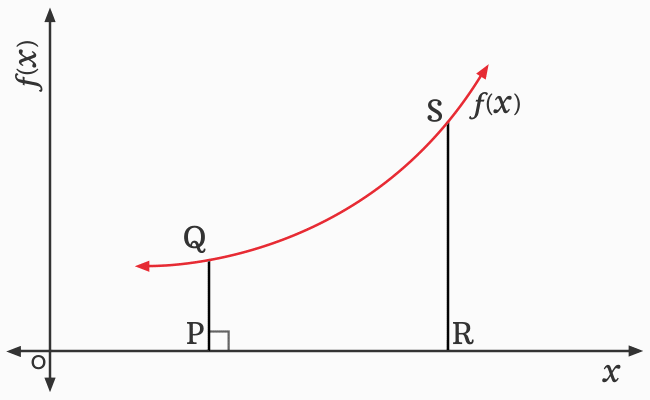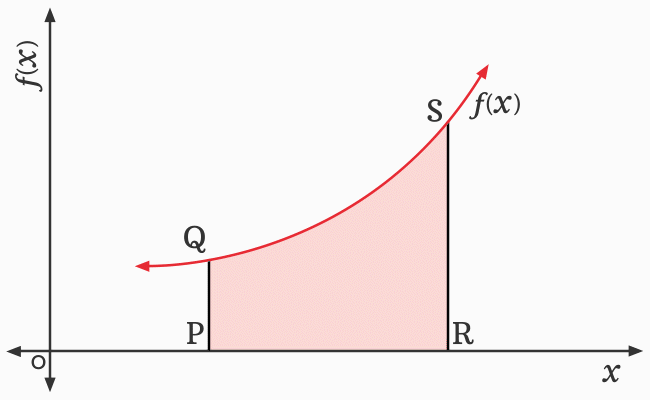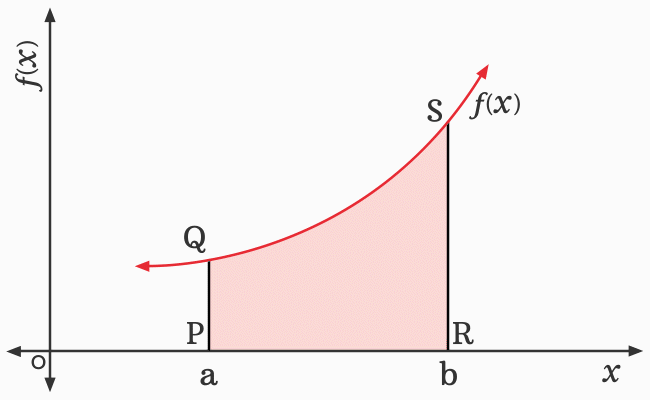
A graph of a function is required to explain the concept of definite integral in geometrical system. So, let us draw a graph for a function firstly and then, take few more geometric steps for preparing the graph to support the geometrical interpretation.

1. Let $x$ be a variable and it represents the real numbers on horizontal $x$-axis.
2. Let’s consider a function and it is a function in terms of $x$. So, it is written as $f(x)$ in mathematics. The corresponding values of the function for all values of $x$ are represented on vertical $y$-axis. Thus, the mathematical relationship between the values of $x$ and corresponding values of the function $f(x)$ is expressed by a curve.
3. Now, consider a point $P$ on $x$-axis and draw a straight line to intersect the curve at point $Q$. Similarly, consider another point on $x$-axis, denoted by $R$ and then, draw a straight line to intersect the curve at point $S$. Remember, the two straight lines should be perpendicular to the horizontal axis.
4. Assume that the $x$-coordinate of the points $P$ and $R$ are denoted by $a$ and $b$ respectively.

Interpretation

A closed geometric shape $PQSR$ is formed. The area of the closed geometric shape is equal to the area bounded by the curve of the function $f(x)$, the lines $x = a$ and $x = b$, and the $x$-axis.

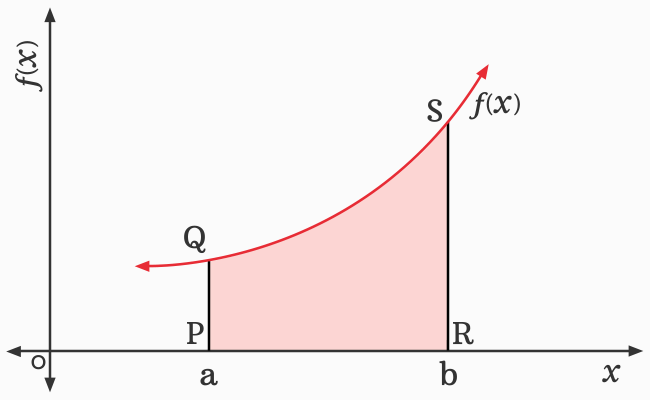
The region $PQSR$ is not a perfect quadrilateral. So, it is not possible to find the area of the region by the area formulas because it is neither a square nor a rectangle nor any other quadrilateral. However, splitting the region into several rectangles of same length helps us to find its area. So, split the region into several rectangles of same length, as displayed in the picture.

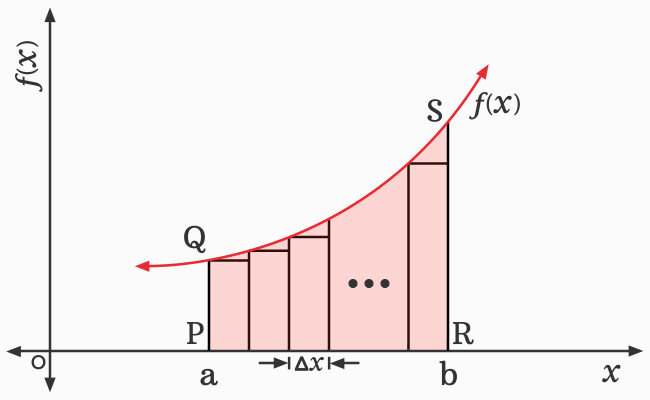
Now, the length of every rectangle is equal, and it can be denoted by a differential element $\Delta x$ as per differential calculus, but the width of every rectangle is different. However, the area of every rectangle can be calculated by its area formula. Integrating the areas of all rectangles is the concept of finding the whole area of the region $PQSR$.

The area of every rectangle can be calculated easily by the area formula of a rectangle but we can notice that we are ignoring some portions of the region over rectangles. For that reason, the sum of areas of all rectangles is not exactly equal to the area of the closed geometric shape $PQSR$.

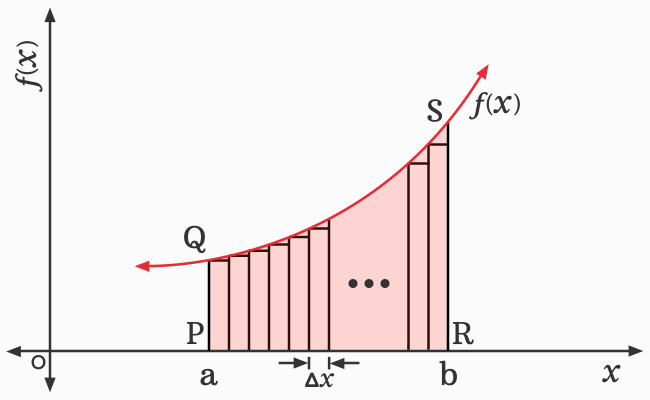
If we reduce the length of every rectangle to half, then the ignored portion of the region over all rectangles is reduced when compared to the previous case. Now, the sum of areas of all rectangles is closer to the area of the region $PQSR$ but not exactly equal. However, the sum of areas of all rectangles of current case is greater than the areas of all rectangles of previous case.

The two cases have cleared that reducing the length of a rectangle minimizes the neglected area over every rectangle. Therefore, if the length of every rectangle is approximately zero, then the neglected area over every rectangle is also equal to zero. In that case, the sum of areas of all rectangles is exactly equal to the area of the closed geometric shape $PQSR$.

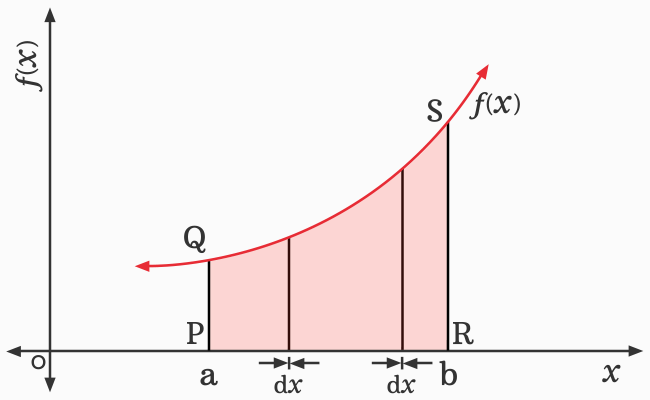
Now, split the area of the region $PQSR$ into several rectangles of same length.

1. The length of each rectangle is very small, which is approximately equal to zero and its length is mathematically denoted by a differential $dx$. Due to the very small length, the rectangle is appearing like a straight line. Remember, we are showing only two rectangles for our convenience in the picture.
2. The width of every rectangle is variable and it can be recognized by comparing the widths of the two rectangles. However, the width of every rectangle can be calculated by the function $f(x)$.

Therefore, the area of one rectangle is the product of the length and width of the rectangle.

$A_R$ $\,=\,$ $dx \times f(x)$

$\implies$ $A_R$ $\,=\,$ $f(x) \times dx$

$\,\,\,\therefore\,\,\,\,\,\,$ $A_R$ $\,=\,$ $f(x)dx$

The area of every rectangle is expressed by the above formula mathematically. So, add the areas of all rectangles and the summation of them is denoted by the integral symbol in calculus.

$\implies$ $A$ $\,=\,$ $\displaystyle \int{f(x)}\,dx$

The function $f(x)$ is a continuous function. So, the curve continues infinitely in both directions. The integral of the product of $f(x)$ and $dx$ calculates the area under the whole curve.

In this case, the area under the curve should be calculated between the limits. So, the bounds should be defined to find the integral of the function. For that reason, the bounds $a$ and $b$ are displayed below and above the integral symbol respectively.

$\,\,\,\therefore\,\,\,\,\,\,$ $A$ $\,=\,$ $\displaystyle \int_{\displaystyle a}^{\displaystyle b}{f(x)}\,dx$

The integral of the function $f(x)$ from $a$ to $b$ is exactly calculates the area bounded by the curve $f(x)$, lines $x = a$ and $x = b$, and the horizontal $x$-axis.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.