Equation of a circle centered at the origin
Fact-checked:
Equation
$x^2+y^2 \,=\, r^2$
Introduction
A circle without touching any axis of the two dimensional cartesian coordinate system is a standard form a circle and its circle is called the equation of a circle in standard form.
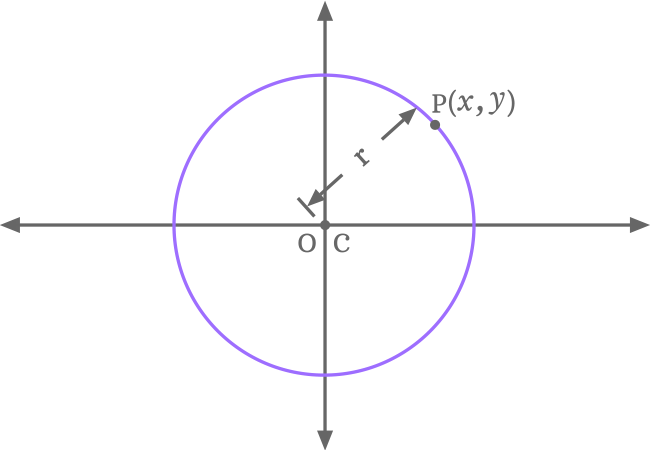
Let $C$ represents the center (or centre) of a circle, $P$ represents a point on the circumference of the circle and $r$ represents the radius of circle.
Let $a$ and $b$ be $x$ and $y$ coordinates of center (or centre) and the center in coordinate form is written as $C(a, b)$. Similarly, $x$ and $y$ be the horizontal and vertical coordinates of point $P$ and it is written as $P(x, y)$ in coordinate form.
The equation of a circle in standard form is written in mathematics as follows.
$x^2+y^2 \,=\, r^2$
Proof
Learn how to derive the equation of a circle in general form when the circle does not touch both axes.

