Corresponding Angles formed by Nonparallel Lines and their transversal

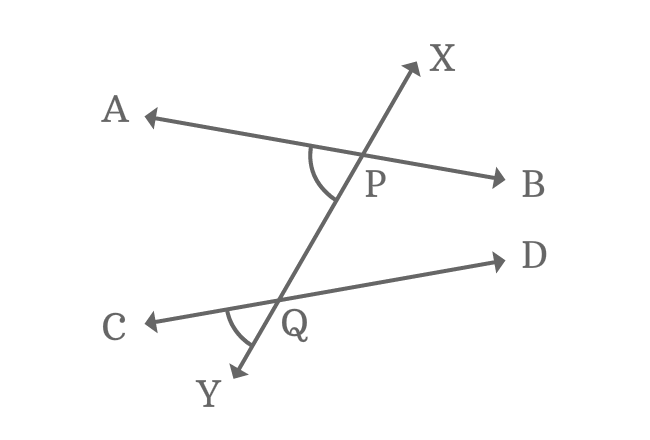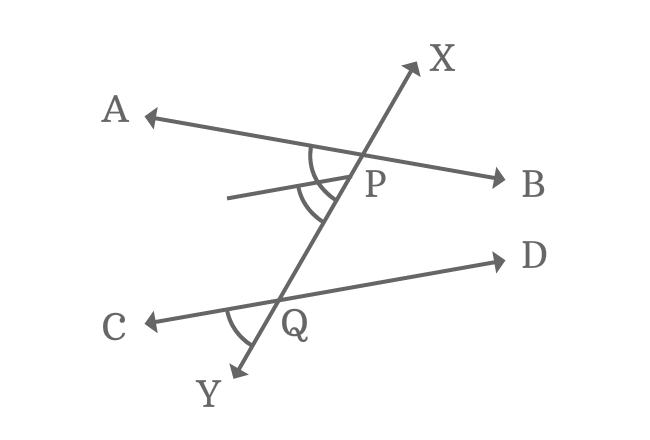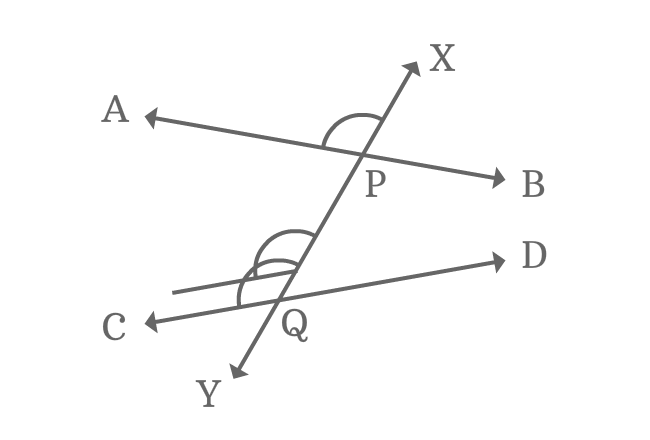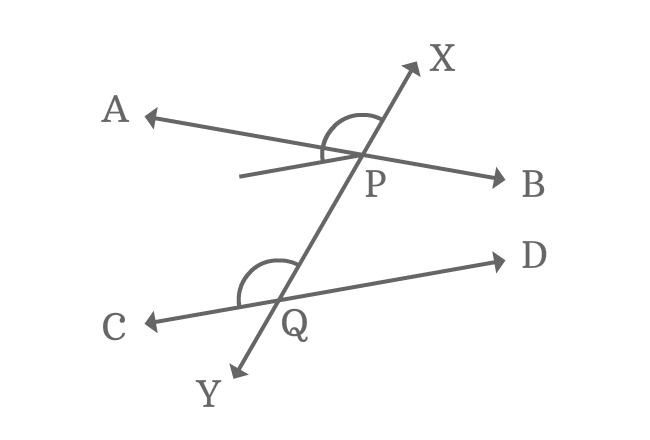
Four pairs of angles have similar relative position at every intersection of every two straight lines when two nonparallel lines are intersected by their transversal. The angles are known as corresponding angles of the transversal of nonparallel lines.

Observe the picture, an angle has similarity in position with another angle and each pair of such angles are known as corresponding angles. Four pairs of corresponding angles are formed geometrically when a pair of nonparallel lines are cut by their transversal.

Property

Geometrically, the corresponding angles which have similar relative position are not equal when two non-parallel lines are intersected by their transversal and this property can also be proved in geometric system.

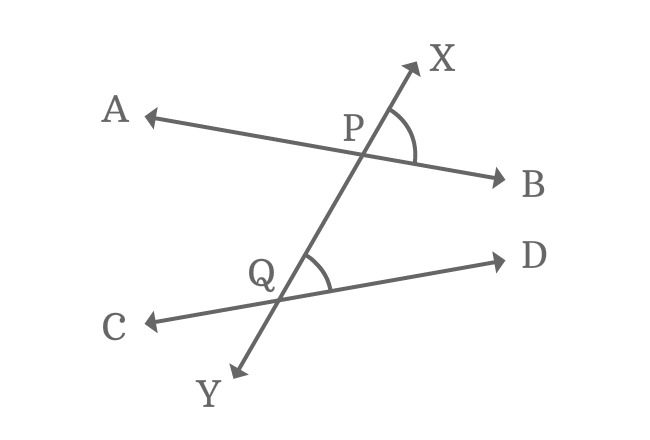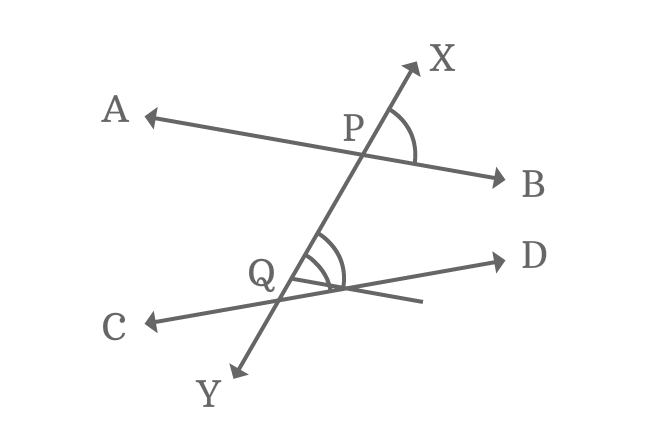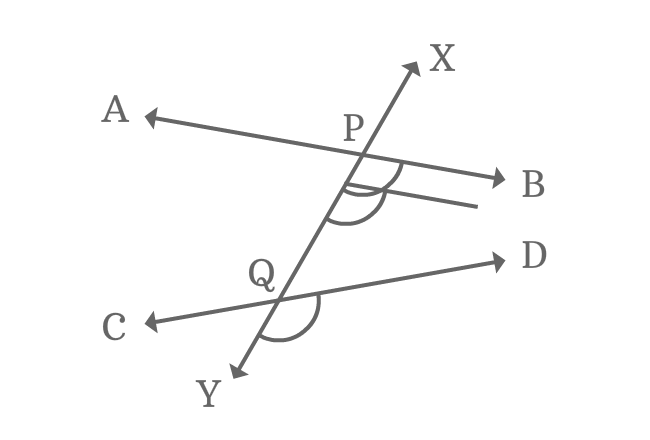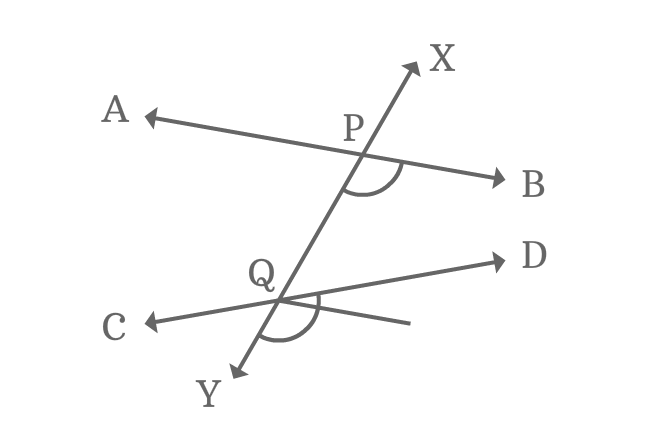
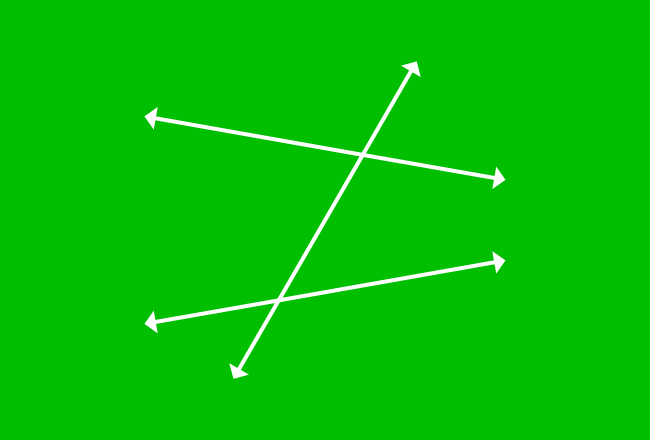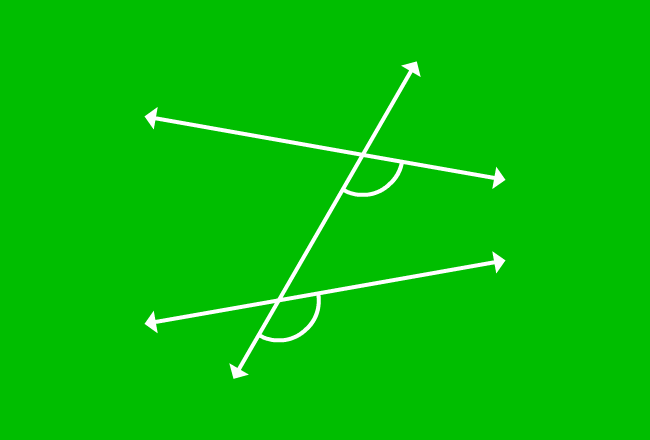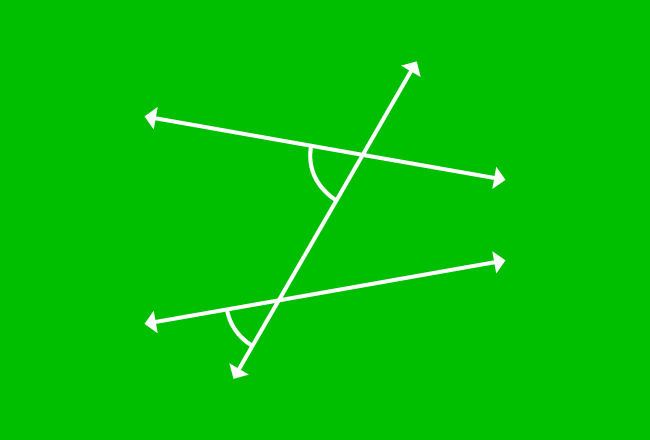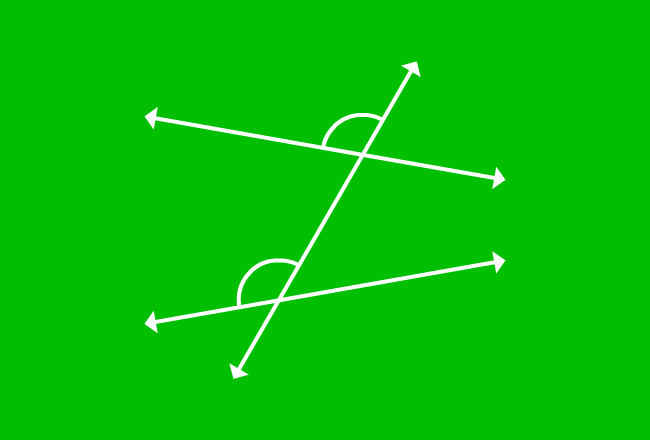
$\angle XPB$ and $\angle XQD$ are similar in relative position. So, they are corresponding angles but they both are not equal geometrically.

$\angle XPB \ne \angle XQD$

It is mainly due to the intersection of the two nonparallel lines by their transversal.

In the same way, the second set of corresponding angles $\angle YPB$ and $\angle YQD$ are also not equal.

$\angle YPB \ne \angle YQD$

$\angle YQC$ and $\angle YPA$ are another set of corresponding angles and they are also not equal.

$\angle YQC \ne \angle YPA$

Similarly, the corresponding angles $\angle XQC$ and $\angle XPA$ are also not equal.

$\angle XQC \ne \angle XPA$

So, the animation tutorial is demonstrated that each pair of corresponding angles are not equal geometrically when two nonparallel lines are cut by their transversal.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.