Proof of Commutative property of Multiplication

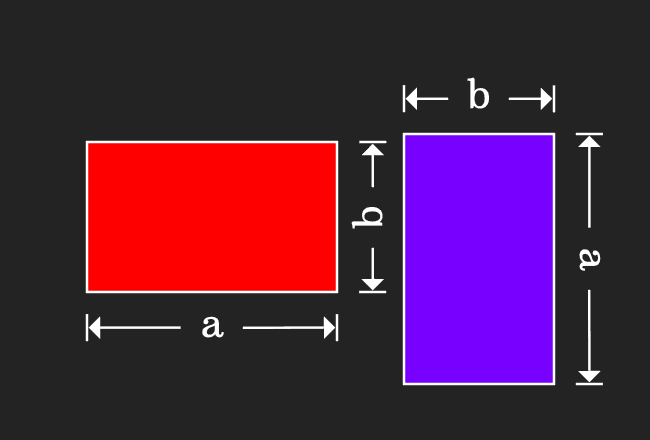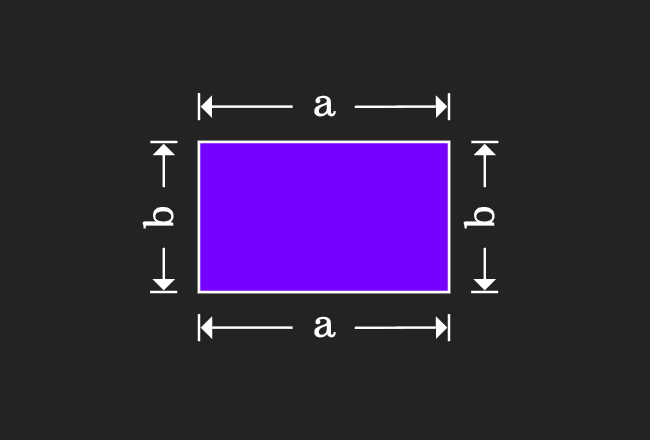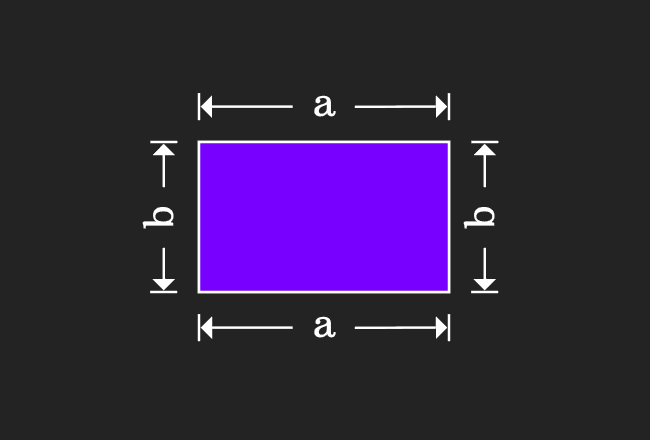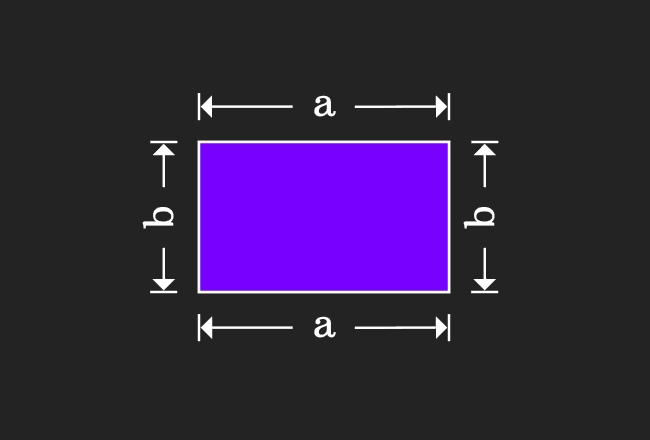
The commutative law of multiplication can be proved in algebraic form by the geometrical approach. In this geometric method, the areas of two rectangles are expressed in algebraic form and then the relationship between them is analyzed mathematically for expressing the commutative rule of multiplication in mathematical form.

Calculate the Area of a Rectangle

We are about to construct a rectangle in this step for finding its area in algebraic form.

1. Draw a rectangle shape.
2. Take, the length of the rectangle is equal to $a$ units.
3. Take, the width of the rectangle is equal to $b$ units.
4. Now, find the area of the rectangle. It is equal to the product of its length and width. Therefore, the area of the rectangle is $a \times b$ and it is simply written as $a.b$ or $ab$ algebraically.

Calculate the Area of another Rectangle

In this step, we are going to draw another rectangle for evaluating its area mathematically.

1. Now, draw a rectangle in such a way that its length is equal to $b$ units and width is equal to $a$ units.
2. Let us calculate the area of this rectangle. Therefore, the area of this rectangle is equal to $b \times a$, which can be written in mathematical form as $b.a$ or $ba$.

Property of the equality

Now, let us compare them to understand the property of the equality.

In the first step, it is calculated that the area of a rectangle is $a \times b$. Similarly, it is also calculated that the area of another rectangle is $b \times a$ but geometrically the areas of both rectangles are equal.

$\implies$ $a \times b$ $\,=\,$ $b \times a$

$\implies$ $a.b$ $\,=\,$ $b.a$

$\,\,\, \therefore \,\,\,\,\,\,$ $ab$ $\,=\,$ $ba$

Therefore, it is proved that the product of any two operands is equal to the product of the same operands in reverse order. The law is called as the commutative property of multiplication.