The commutative law of addition can be derived in algebraic form by the geometrical approach. In this method, the lengths of line segments are expressed in algebraic form and they are joined geometrically for proving the commutative rule of addition in algebraic form.
We are going to draw a line segment geometrically in this step by connecting two line segments.

In this step, we are about to draw another line segment by joining two line segments.
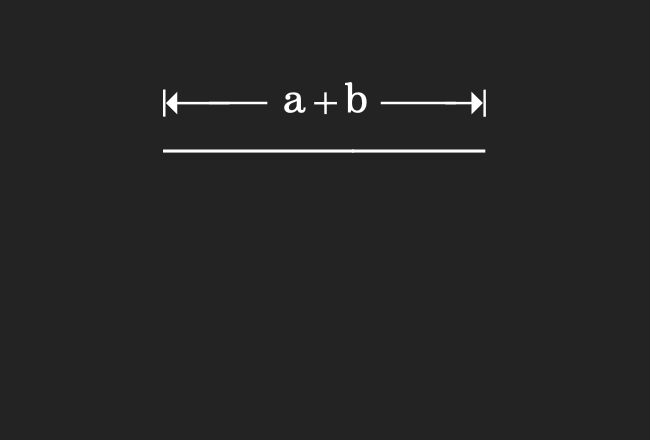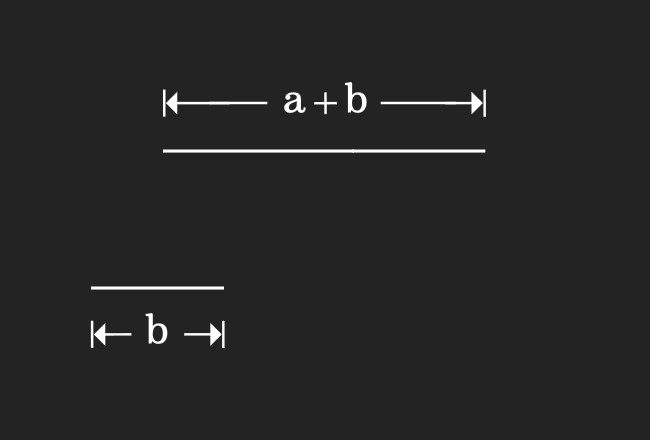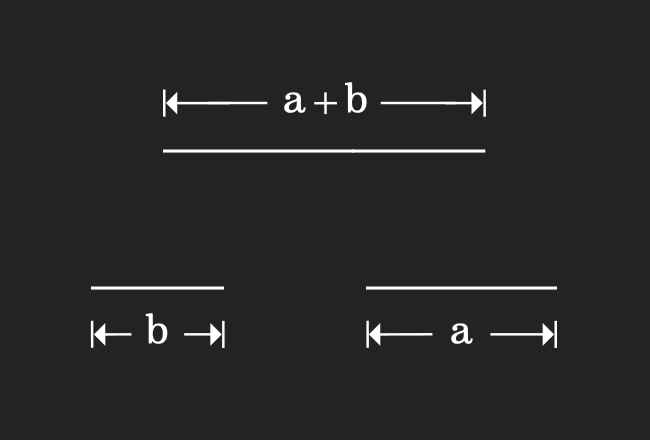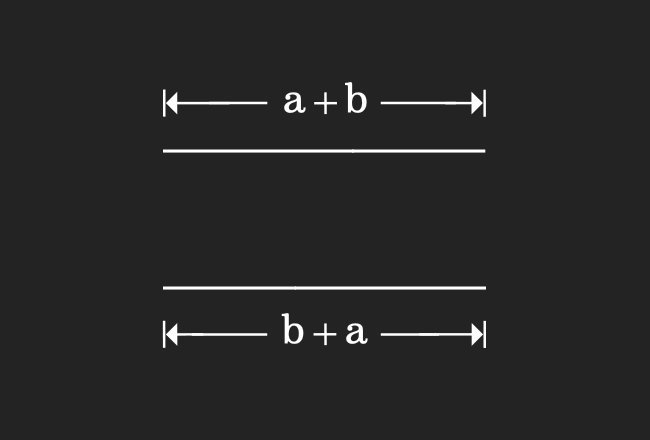
Finally, we compare the lengths of both line segments in this step for proving the commutative rule of the addition.
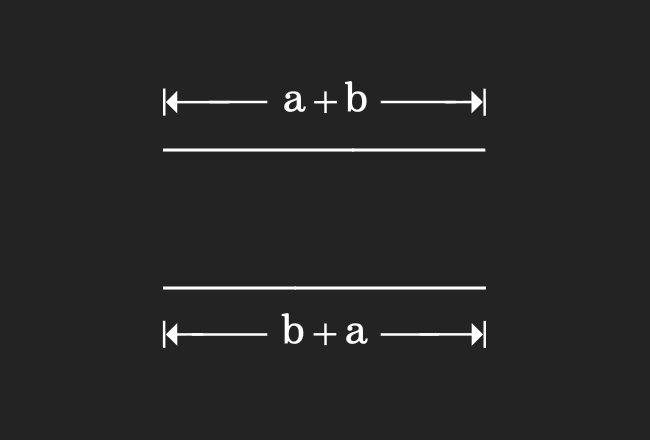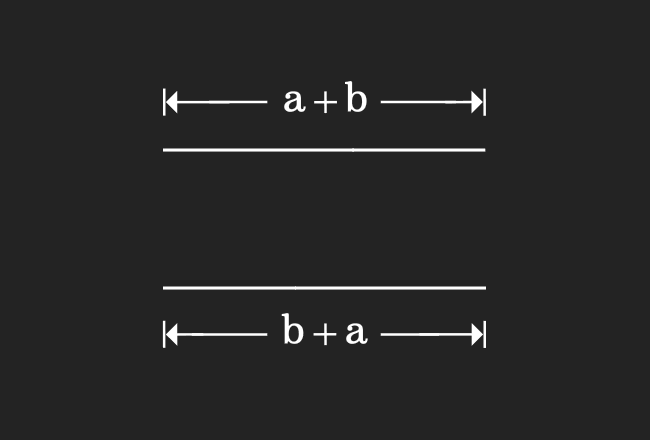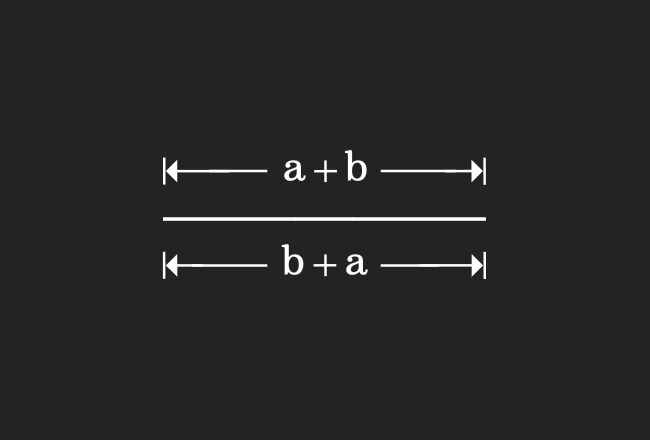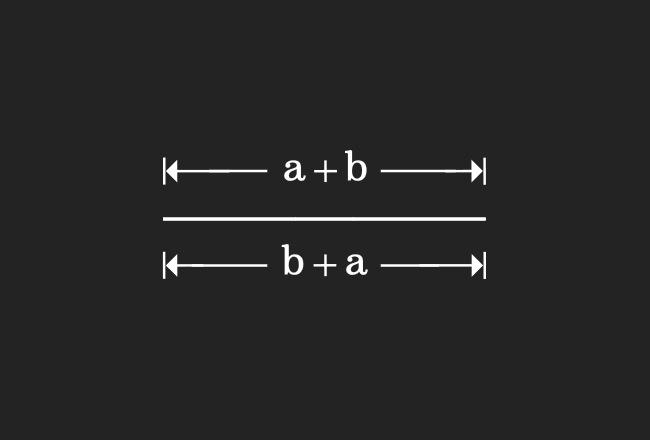
In the first step, we have drawn a line segment and its length is $a+b$. We have also drawn another line segment in the second step and its length is $b+a$. When we compare them, it clears that the lengths of them are equal geometrically.
$\therefore \,\,\,\,\,\,$ $a+b$ $\,=\,$ $b+a$
The expression in the left hand side of the equation represents the sum of two quantities and the same two operands are in reverse order in the right hand side expression.
However, it expresses that they both are equal geometrically and this law is called the commutative property of addition.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved