Equation of a Circle when the circle touches the y-axis

An equation that represents a circle when the circle touches the $y$-axis at a point is called the equation of a circle touching the $y$-axis.

Introduction

A circle touches the vertical axis at a point in a special case and it can be expressed mathematically in a mathematical equation.

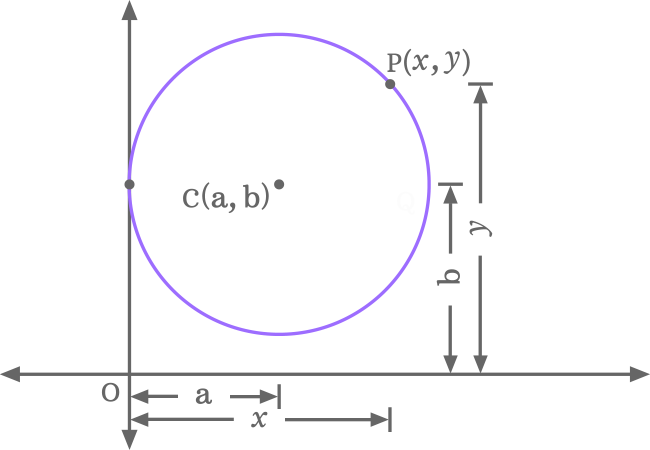
Let $C$ be a center (or centre) be a point on the circumference of a circle. The centre $C$ with its coordinates is written as $C(a, b)$ in mathematical form if the horizontal and vertical distances of the centre $C$ are $a$ and $b$ units from the origin.

Let us assume that a point on the circumference of circle is denoted by $P$. The point $P$ in coordinate form is written as $P(x, y)$ mathematically if the horizontal and vertical distances of the point $P$ are $x$ and $y$ units from the origin.

Simple form

$(x-a)^2+(y-b)^2 \,=\, a^2$

Expansion

$x^2+y^2\,-\,2ax\,\,–\,2by+b^2 \,=\, 0$

Alternative form

If the coordinates of the center (or centre) are denoted by $h$ and $k$, then the centre in coordinate form is written as $C(h, k)$. Therefore, the above circle’s equations are written as follows.

Simple form

$(x-h)^2+(y-k)^2 \,=\, h^2$

Expansion

$x^2+y^2\,-\,2hx\,\,–\,2ky+k^2 \,=\, 0$

Proof

Learn how to derive the equation of a circle when the circle is touching the $y$-axis.