Geometric proof of Area of an Annulus

The formula for finding the area of an annulus (or a circular ring) is written as follows.

$A$ $\,=\,$ $\pi(R^2-r^2)$

It can be derived in mathematical form geometrically. Let’s learn how to find the area of a circular ring (or an annulus) by the geometrical approach.

Areas of the circles

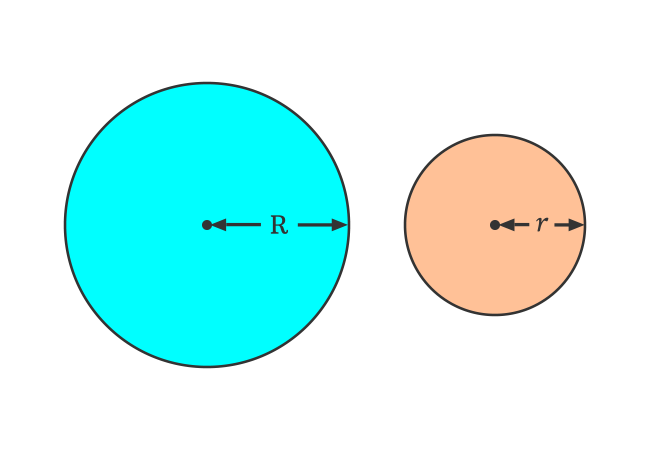
Firstly, consider two circles and their radii are different. The radius of one circle is denoted by $R$ and the radius of the second circle is represented by $r$. Here, $R \,>\, r$

Similarly, the areas of both circles are denoted $A_1$ and $A_2$ respectively. According to the area of a circle formula, the area of each circle can be written as follows.

$(1).\,\,\,$ $A_1 \,=\, \pi R^2$

$(2).\,\,\,$ $A_2 \,=\, \pi r^2$

Area of the concentric circles

The two circles are arranged in such a way that the centers of them coincide at a point. The concentric circles have a common centre and their subtraction forms a geometric shape, called an annulus or a circular ring. Let’s denote its area by $A$.

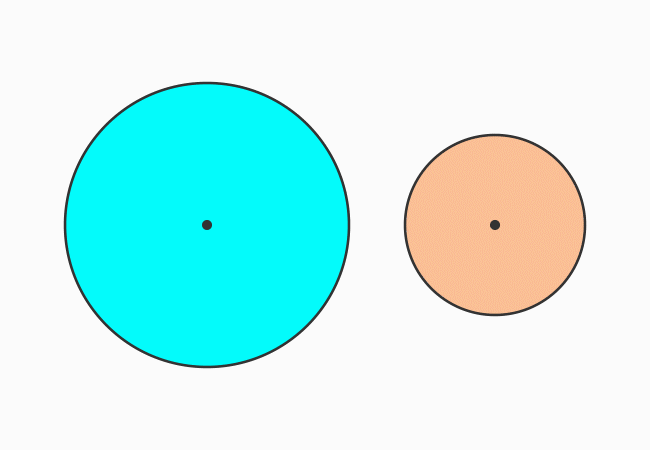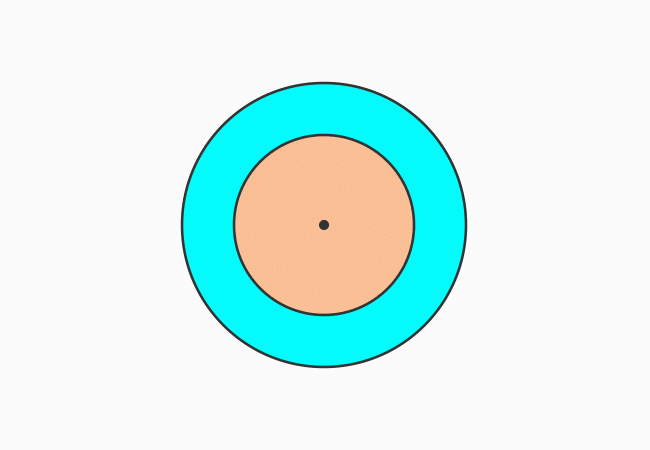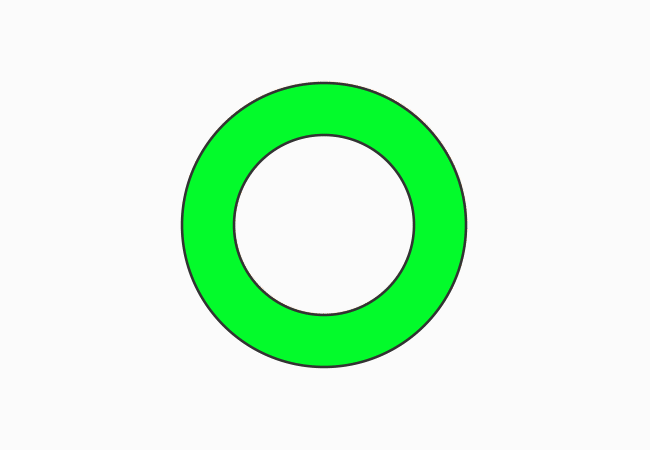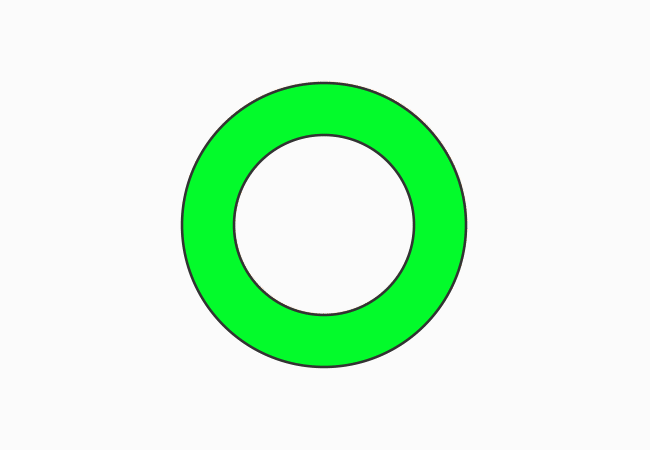
The area of circular ring can be obtained by subtracting the area of the small circle from the area of the big circle.

$A$ $\,=\,$ $A_1-A_2$

Now, substitute areas of both circles in mathematical form in the above equation.

$\implies$ $A$ $\,=\,$ $\pi R^2-\pi r^2$

$\implies$ $A$ $\,=\,$ $\pi \times R^2-\pi \times r^2$

Pi is a common factor in both terms on the right hand side of the equation. It can be taken out common from them for simplifying the expression further.

$\implies$ $A$ $\,=\,$ $\pi \times (R^2-r^2)$

$\,\,\,\therefore\,\,\,\,\,\,$ $A$ $\,=\,$ $\pi(R^2-r^2)$

It is a formula to find the area of an annulus or a circular ring from the radii of the two concentric circles.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.