Adjacent sides of a Quadrilateral

The sides, which have a common vertex in a quadrilateral are called the adjacent sides of a quadrilateral.

Introduction

There are four line-segments in a quadrilateral. The endpoint of one line segment is connected to the endpoint of another line segment to form a closed geometric shape. Thus, every two sides are connected at an intersecting point, called a vertex, and the two sides are called the adjacent sides of a quadrilateral.

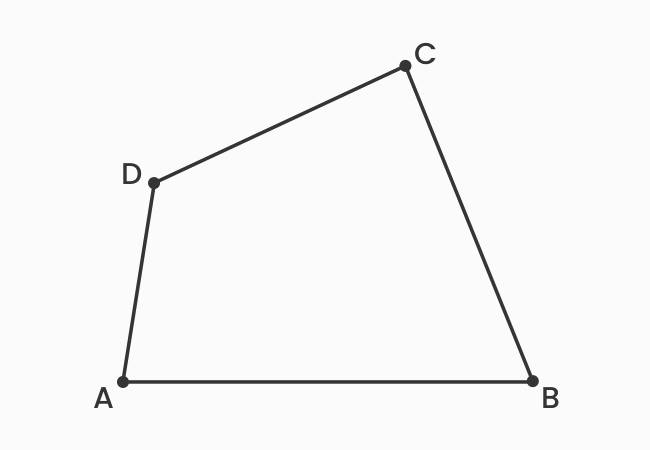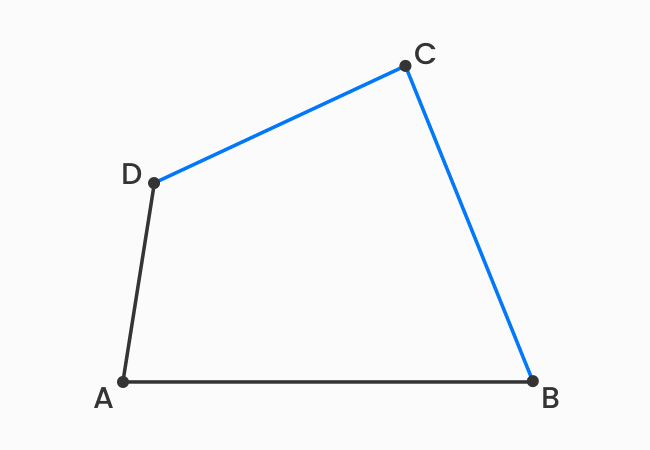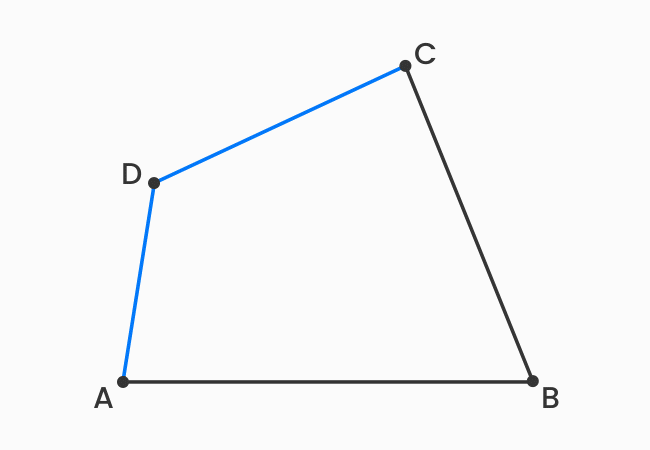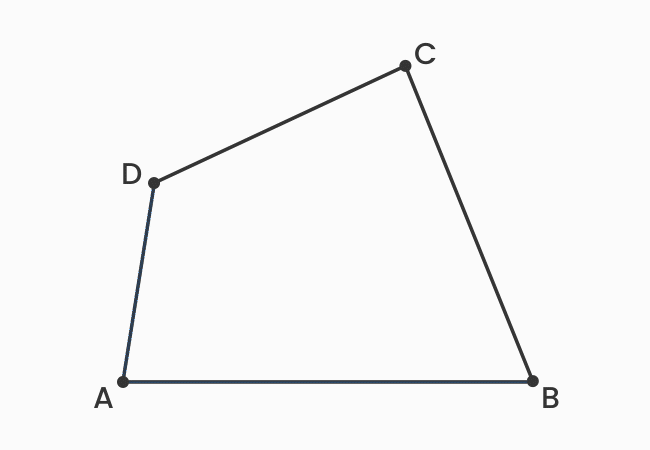
The adjacent sides are also called the consecutive sides of a quadrilateral. There are four pairs of consecutive sides in a quadrilateral. Now, let’s identify four pairs of adjacent sides in a quadrilateral.

1. The sides $\small \overline{AB}$ and $\small \overline{BC}$ have a common intersecting point at point $\small B$. So, the sides $\small \overline{AB}$ and $\small \overline{BC}$ are called the adjacent sides of quadrilateral.
2. The sides $\small \overline{BC}$ and $\small \overline{CD}$ have a vertex at point $\small C$. So, the sides $\small \overline{BC}$ and $\small \overline{CD}$ are called the consecutive sides of quadrilateral.
3. The sides $\small \overline{CD}$ and $\small \overline{DA}$ have a common meeting point at point $\small D$. So, the sides $\small \overline{CD}$ and $\small \overline{DA}$ are called the adjacent sides of quadrilateral.
4. The sides $\small \overline{DA}$ and $\small \overline{AB}$ have a vertex $\small D$ commonly. Therefore, the sides $\small \overline{DA}$ and $\small \overline{AB}$ are called the consecutive sides of quadrilateral.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.