Acute triangle

A triangle which contains acute angles as its three interior angles is called an acute triangle (or) acute angled triangle.

Introduction

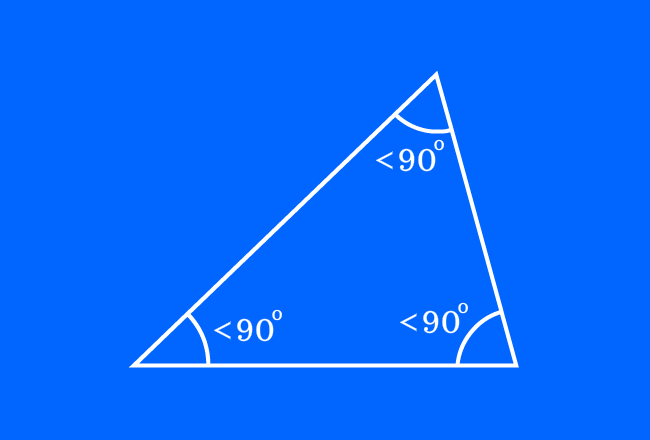
A triangle usually contains three interior angles by the intersection of three sides. Sometimes, every interior angle in a triangle can be an acute angle, which means less than $90^\circ$.

This type of triangle is called as an acute triangle and also called as an acute angled triangle.

Example

$\Delta ABC$ is a triangle and its three interior angles are measured as follows.

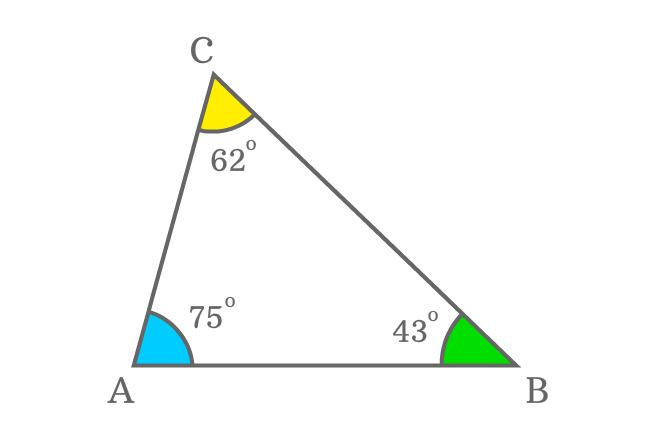
$(1)\,\,\,\,\,\,$ $\angle ABC = 43^\circ$

$(2)\,\,\,\,\,\,$ $\angle BCA = 62^\circ$

$(3)\,\,\,\,\,\,$ $\angle CAB = 75^\circ$

It is observed that a property is common in all three angles. In other words, every interior angle is less than $90$ degrees. So, each interior angle in this triangle is an acute angle. Therefore, the ABC is a best example for an acute triangle.