An angle of less than $90^\circ$ is called an acute angle

The meaning of acute is, an angle of less than $90^\circ$. Therefore, if any angle is less than $90^\circ$, the angle is called as an acute angle geometrically.
Zero angle is a best example of an acute angle because the range of acute angle starts from zero degrees and ends just before $90^\circ$.
Mathematically, the range of an acute angle can be expressed as $[0^\circ, 90^\circ)$.
Acute angles are geometrically formed in two different possible cases.
Angle of any line is measured from the zero degrees because it is parallel to the surface of the earth.
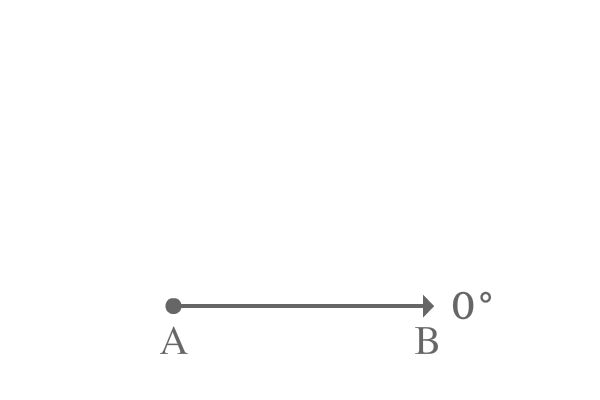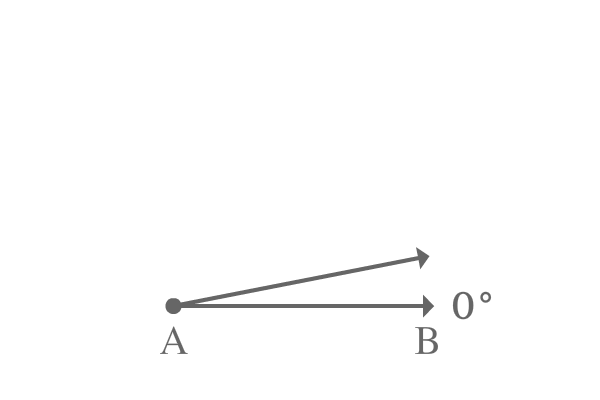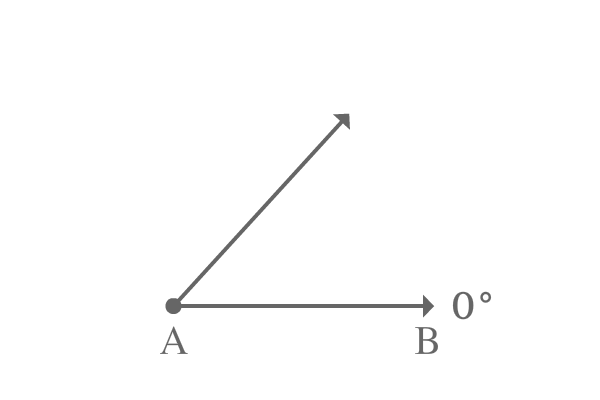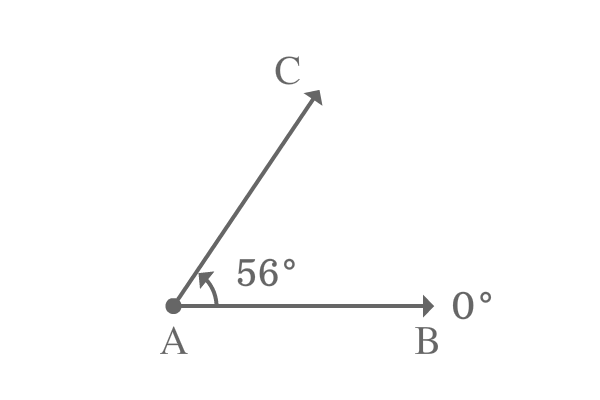
$\overrightarrow{AB}$ is a ray and it is initially at $0^\circ$ angle. Later, the ray $\overrightarrow{AB}$ is rotated an angle of $56^\circ$ in anticlockwise direction to become $\overrightarrow{AC}$ at its final position.
The ray $\overrightarrow{AB}$ is made an angle of $56^\circ$ to reach its final position from its initial position.
$\angle CAB = 56^\circ$
The angle $CAB$ is less than $90^\circ$. Therefore, the $\angle CAB$ is called as an acute angle.

$\overrightarrow{DE}$ and $\overrightarrow{DF}$ are two rays and they both started from point $D$.
The two rays have a common vertex and an angle is formed between them. The angle between them is measured by considering one ray as baseline to measure the angle of another ray and vice-versa.
The angle between them is measured as $38^\circ$.
$\angle EDF = 38^\circ$
The angle $EDF$ is less than $90^\circ$. Therefore, it is called as an acute angle geometrically.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved