$\tan{\theta}\cot{\theta} \,=\, 1$
The tangent and cotangent functions are reciprocal function mathematically. Therefore, the product of them equals to one and the product relation between tan and cot functions can also be proved in trigonometric mathematics.
$\Delta QPR$ is a right triangle and the angle of this triangle is theta ($\theta$).
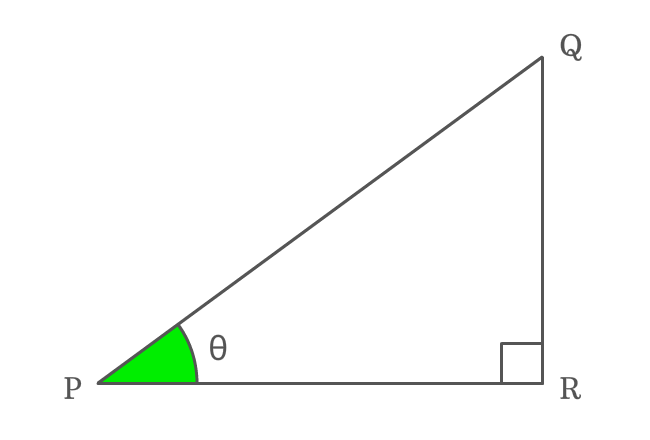
Express tangent function ($\tan{\theta}$) in its ratio form firstly.
$\tan{\theta} \,=\, \dfrac{QR}{PR}$
After that, write cotangent function ($\cot{\theta}$) in its ratio form.
$\cot{\theta} \,=\, \dfrac{PR}{QR}$
Lastly, multiply both tan and cot functions to obtain product of them.
$\tan{\theta} \times \cot{\theta}$ $\,=\,$ $\dfrac{QR}{PR} \times \dfrac{PR}{QR}$
$\implies$ $\tan{\theta} \times \cot{\theta}$ $\,=\,$ $\dfrac{QR \times PR}{PR \times QR}$
$\implies$ $\tan{\theta} \times \cot{\theta}$ $\,=\,$ $\require{cancel} \dfrac{\cancel{QR} \times \cancel{PR}}{\cancel{PR} \times \cancel{QR}}$
$\,\,\, \therefore \,\,\,\,\,\,$ $\tan{\theta}.\cot{\theta} \,=\, 1$
Therefore, it is proved mathematically that the product of tan and cot functions at an angle is equal one, and this property is used in trigonometry as a formula.
One important thing is the angle of a right triangle can be denoted by any symbol but the product of tangent of angle and cotangent of angle always equals to one.
For example, if $x$ represents angle of right triangle, then
$\tan{x}.\cot{x} \,=\, 1$
Similarly, if $A$ is used to denote angle of right triangle, then
$\tan{A}.\cot{A} \,=\, 1$
The tangent and cotangent functions in the product trigonometric identity can be written in terms of any angle but the product of them equals to one mathematically.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved