Product identity of Sine and Cosecant functions

Formula

$\sin{\theta}\csc{\theta} \,=\, 1$

Proof

Sine and Cosecant functions are reciprocals mathematically. Hence, their product should be equal to one. The product relation between sine and cosecant functions can also be proved in trigonometry.

$\Delta RPQ$ is a right triangle and its angle is taken as theta.

Write sine function in ratio form

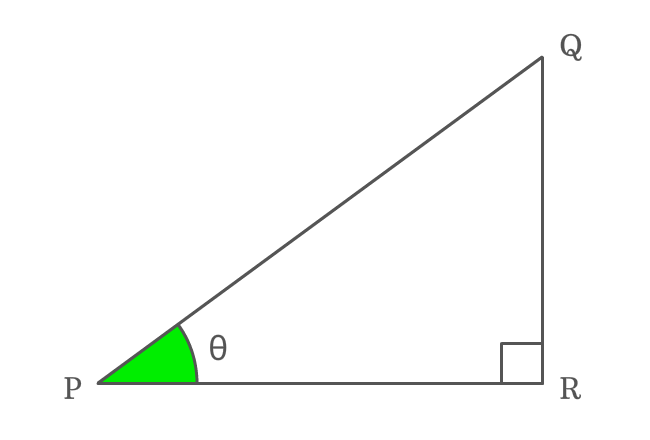
Firstly, write sin function ($\sin{\theta}$) in its ratio form.

$\sin{\theta} \,=\, \dfrac{QR}{PQ}$

Write cosecant function in ratio form

Similarly, write cosecant function ($\csc{\theta}$ or $\operatorname{cosec}{\theta}$) in its ratio form.

$\csc{\theta} \,=\, \dfrac{PQ}{QR}$

Find Product of sine and cosecant

Multiply both sine and cosecant functions to evaluate product of them.

$\sin{\theta} \times \csc{\theta}$ $\,=\,$ $\dfrac{QR}{PQ} \times \dfrac{PQ}{QR}$

$\implies$ $\sin{\theta} \times \csc{\theta}$ $\,=\,$ $\dfrac{QR \times PQ}{PQ \times QR}$

$\implies$ $\sin{\theta} \times \csc{\theta}$ $\,=\,$ $\require{cancel} \dfrac{\cancel{QR} \times \cancel{PQ}}{\cancel{PQ} \times \cancel{QR}}$

$\,\,\, \therefore \,\,\,\,\,\,$ $\sin{\theta}.\csc{\theta} \,=\, 1$

Therefore, it is proved that the product of sin and cosecant functions at an angle is equal one, and this trigonometric property is used as a formula in mathematics.

Note

Remember, the angle of a right triangle can be denoted by any symbol but the product of sin of angle and cosecant of angle is always equal to one.

For example, if $x$ represents angle of right triangle, then

$\sin{x}.\csc{x} \,=\, 1$

Similarly, if $A$ is used to represent angle of right triangle, then

$\sin{A}.\csc{A} \,=\, 1$

The sine and cosecant functions in the trigonometric product identity can be expressed in terms of any angle but the product of them is equal to one mathematically.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.