The angle sum tan identity is a trigonometric identity, used as a formula to expanded tangent of sum of two angles. For example, $\tan{(A+B)}$, $\tan{(x+y)}$, $\tan{(\alpha+\beta)}$, and so on. You know the tan of sum of two angles formula but it is very important for you to know how the angle sum identity is derived in mathematics.
The tan of angle sum identity is actually derived in mathematical form by the geometrical method. It is actually done on the basis of a right triangle but its angle is divided as sum of two angles for expressing the tan of sum of two angles.
The $\Delta FEG$ is a right triangle and its angle is divided as two angles to derive the tan of angle sum identity in mathematical form by the geometrical approach.
$(1). \,\,\,$ To divide $\angle FEG$, draw a straight line to side $\overline{FG}$ from point $E$. It splits the $\angle FEG$ as two angles $x$ and $y$, and also intersects the side $\overline{FG}$ at point $H$.
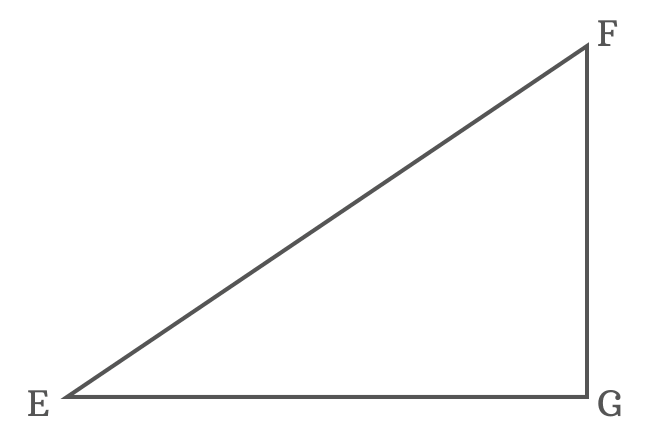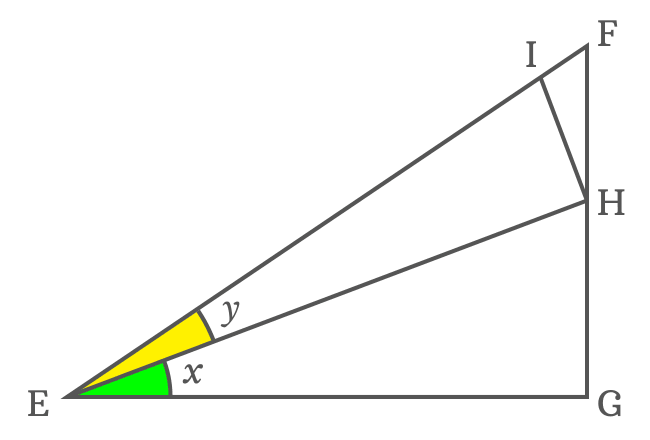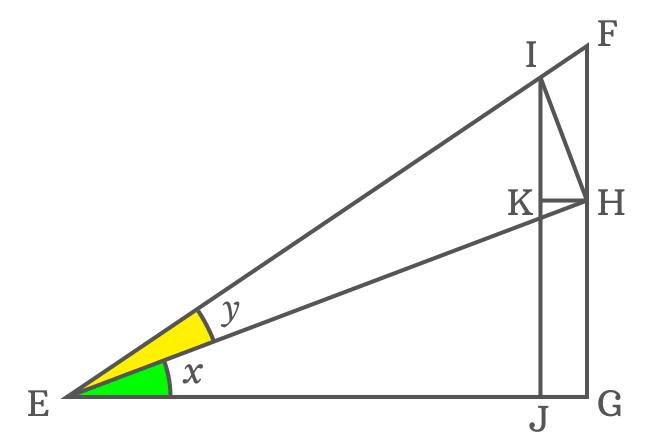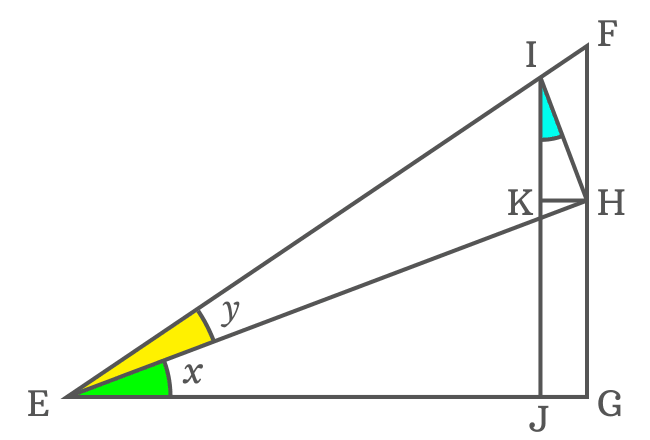
$(2). \,\,\,$ Draw a perpendicular line to side $\overline{EH}$ from $H$ towards side $\overline{EF}$ and it intersects the side $\overline{EF}$ at point $I$. Therefore $\overline{EH} \perp \overline{IH}$
$(3). \,\,\,$ Now, draw a perpendicular line to side $\overline{EG}$ from point $I$ and it intersects the side $\overline{EG}$ at point $J$ perpendicularly.
$(4). \,\,\,$ Draw a perpendicular line to side $\overline{IJ}$ from $H$ and it cuts the side $\overline{IJ}$ at point $K$.
Geometrically, The $\Delta GEH$ with angle $x$, the $\Delta IEH$ with angle $y$ and $\Delta KIH$ with unknown angle are constructed geometrically inside the $\Delta FEG$.
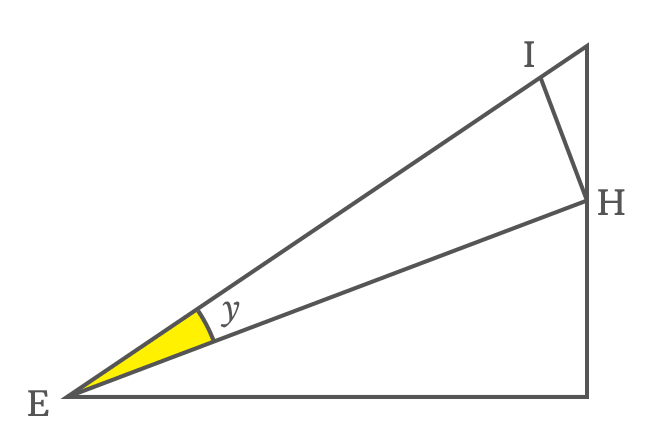
In $\Delta JEI$, the $\angle JEI \,=\, x+y$. Express tangent of compound angle $x+y$ in its ratio form as per this triangle.
$\tan{(x+y)}$ $\,=\,$ $\dfrac{IJ}{EJ}$
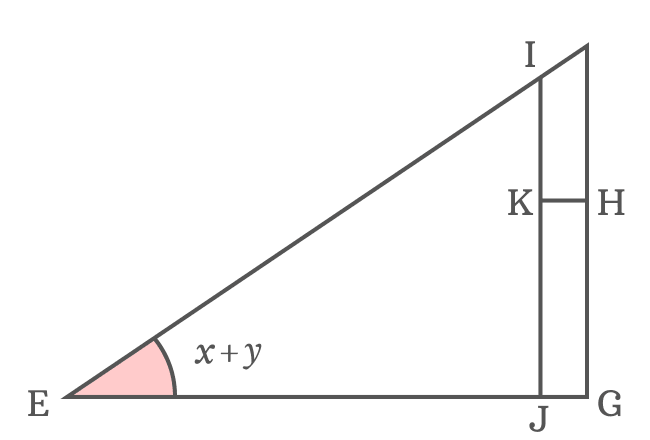
The side $\overline{KH}$ splits the side $\overline{IJ}$ as two sides $\overline{IK}$ and $\overline{KJ}$. Therefore, $IJ \,=\, IK+KJ$.
Similarly, the side $\overline{IJ}$ splits the side $\overline{EG}$ as two sides $\overline{EJ}$ and $\overline{JG}$.
$EG \,=\, EJ+JG$
$\implies EJ \,=\, EG\,–\,JG$
Now, substitute the lengths of the sides $\overline{IJ}$ and $\overline{EJ}$ in the $\tan{(x+y)}$ expansion.
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{IK+KJ}{EG\,–\,JG}$
Actually, the $\overline{KJ}$ and $\overline{HG}$ are parallel lines. So, $KJ = HG$. The sides $\overline{JG}$ and $\overline{KH}$ are parallel lines. Therefore, $JG = KH$. Now, replace $KJ$ by $HG$ and also replace $JG$ by $KH$.
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{IK+HG}{EG\,–\,KH}$
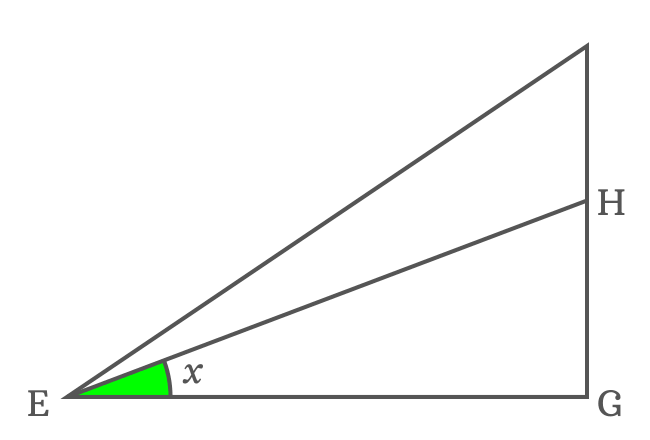
$HG$ is length of the opposite side $\overline{HG}$ in the $\Delta GEH$. Now, try to express $HG$ in the form of a trigonometric function and the angle of the triangle is $x$.
$\tan{x} \,=\, \dfrac{HG}{EG}$
$\implies HG \,=\, {EG}\tan{x}$
Now, replace $HG$ by its equivalent value in the expansion of tan of sum of two angles.
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{IK+{EG}\tan{x}}{EG\,–\,KH}$
$EG$ is a term in both numerator and denominator. Take it common from both terms of the numerator and denominator. It is actually useful to simplify the expansion of $\tan{(x+y)}$ function.
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{{EG}\Bigg[\dfrac{IK}{EG}+\tan{x}\Bigg]}{{EG}\Bigg[1\,–\,\dfrac{KH}{EG}\Bigg]}$
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\require{cancel} \dfrac{\cancel{EG}\Bigg[\dfrac{IK}{EG}+\tan{x}\Bigg]}{\cancel{EG}\Bigg[1\,–\,\dfrac{KH}{EG}\Bigg]}$
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{\dfrac{IK}{EG}+\tan{x}}{1\,–\,\dfrac{KH}{EG}}$
$KH$ is length of the opposite side in $\Delta KIH$. It can be expressed in the form a trigonometric function, same as the above but it is not possible due to unknown angle of the triangle. So, it’s essential to find the $\angle KIH$ for continuing the derivation of tan of angle sum identity.
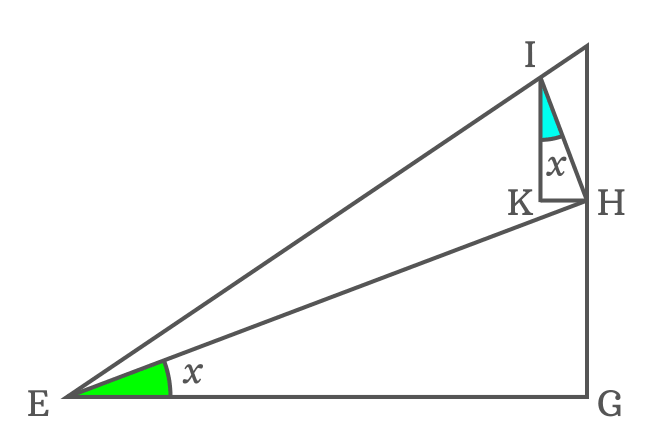
$\overline{KH}$ and $\overline{EG}$ are parallel lines and $\overline{EH}$ is their transversal. The $\angle KHE$ and $\angle GEH$ are alternate interior angles, and they are equal geometrically.
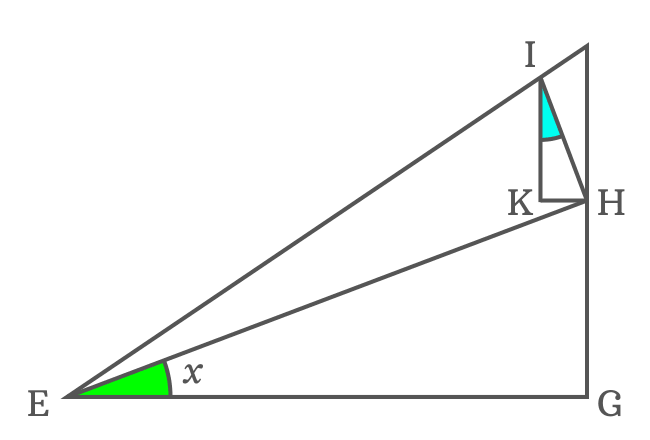
$\angle KHE \,=\, \angle GEH$ but $\angle GEH = x$
$\therefore \,\,\,\,\,\, \angle KHE \,=\, x$
In fact, $\overline{EH} \perp \overline{IH}$. So, $\angle IHE = 90^°$. The side $\overline{KH}$ divides the $\angle IHE$ as two angles $\angle IHK$ and $\angle KHE$.
$\angle IHE \,=\, \angle IHK + \angle KHE$
$\implies 90^° = \angle IHK +x$
$\,\,\, \therefore \,\,\,\,\,\, \angle IHK = 90^°-x$
In $\Delta KIH$, two angles are known and its third angle can be evaluated by using sum of angles of a triangle rule.
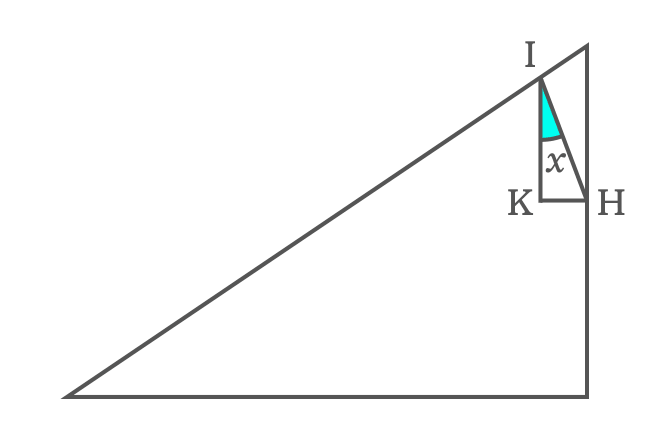
$\angle KIH + \angle IKH + \angle IHK$ $\,=\,$ $180^°$
$\implies$ $\angle KIH + 90^° + 90^°-x$ $\,=\,$ $180^°$
$\implies$ $\angle KIH + 180^°-x$ $\,=\,$ $180^°$
$\implies$ $\angle KIH$ $\,=\,$ $180^°-180^°+x$
$\implies$ $\angle KIH$ $\,=\,$ $\require{cancel} \cancel{180^°}-\cancel{180^°}+x$
$\,\,\, \therefore \,\,\,\,\,\,$ $\angle KIH \,=\, x$
It’s calculated that $\angle KIH = x$ but $\angle GEH$ is also equal to $x$. The two angles are equal because of their congruence property. Therefore, $\Delta KIH$ and $\Delta GEH$ are similar triangles.
Let’s continue deriving the expansion of tan of sum of angles formula.
$\tan{(x+y)}$ $\,=\,$ $\dfrac{\dfrac{IK}{EG}+\tan{x}}{1\,–\,\dfrac{KH}{EG}}$

$KH$ is length of the side $\overline{KH}$ in the $\Delta KIH$. It can be written in the form of tan function.
$\tan{x} \,=\, \dfrac{KH}{IK}$
$\implies KH \,=\, {IK}\tan{x}$
Now, replace the length of the side $\overline{KH}$ by its equivalent value in the $\tan{(x+y)}$ expansion.
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{\dfrac{IK}{EG}+\tan{x}}{1\,–\,\dfrac{{IK}\tan{x}}{EG}}$
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{\dfrac{IK}{EG}+\tan{x}}{1\,–\,\dfrac{IK}{EG}\tan{x}}$
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{\tan{x}+\dfrac{IK}{EG}}{1\,–\,\tan{x} \times \dfrac{IK}{EG}}$
$IK$ is length of the adjacent side of the $\Delta KIH$, and $EG$ is also length of the adjacent side of the $\Delta GEH$. So, they can’t be expressed in terms of tan functions and there is no way to continue further except expressing them in the form of cos functions.
Write $EG$ in terms of cos function according to $\Delta GEH$
$\cos{x} \,=\, \dfrac{EG}{EH}$
$\implies EG \,=\, {EH}\cos{x}$
Similarly, write $IK$ in terms of cos function according to $\Delta KIH$
$\cos{x} \,=\, \dfrac{IK}{IH}$
$\implies IK \,=\, {IH}\cos{x}$
The ratio of $EG$ to $EH$ is equal to the ratio of $IK$ to $IH$ because they both equal to $\cos{x}$.
$\dfrac{EG}{EH} \,=\, \dfrac{IK}{IH}$
$\implies \dfrac{IH}{EH} \,=\, \dfrac{IK}{EG}$
$\implies \dfrac{IK}{EG} \,=\, \dfrac{IH}{EH}$
The quotient of $IK$ by $EG$ can be replaced by the quotient of $IH$ by $EH$ in the expansion of angle sum tan identity.
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{\tan{x}+\dfrac{IH}{EH}}{1\,–\,\tan{x} \times \dfrac{IH}{EH}}$
$IH$ and $EH$ are lengths of the opposite side $\overline{IH}$ and adjacent side $\overline{EH}$ in the $\Delta IEH$. The angle of this triangle is $y$. Now, the ratio between them can be expressed in the form of tan of angle $y$.
$\tan{y} \,=\, \dfrac{IH}{EH}$
Now, replace the ratio of $IH$ to $EH$ by $\tan{y}$ in the expansion of tan of compound angle $x+y$.
$\implies$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{\tan{x}+\tan{y}}{1\,–\,\tan{x} \times \tan{y}}$
$\,\,\, \therefore \,\,\,\,\,\,$ $\tan{(x+y)}$ $\,=\,$ $\dfrac{\tan{x}+\tan{y}}{1\,–\,\tan{x}\tan{y}}$
It is proved the tan of sum of two angles is equal to the quotient of sum of tangents of both angles by the subtraction of products of tangents of both angles from one.
The expansion of tan of sum of two angles is called as angle sum identity for the tan function and also called as tan of compound angle identity. It is used as a trigonometric formula in mathematics.
Remember, the tan of angle sum identity can also be written in terms of any two symbols.
For example, if $A$ and $B$ are two angles, then tan of angle sum function is written as $\tan{(A+B)}$ and it’s expanded in mathematics as follows.
$\tan{(A+B)}$ $\,=\,$ $\dfrac{\tan{A}+\tan{B}}{1\,–\,\tan{A}\tan{B}}$
Similarly, if $\alpha$ and $\beta$ are two angles, then tan of sum of two angles is written as follows.
$\tan{(\alpha+\beta)}$ $\,=\,$ $\dfrac{\tan{\alpha}+\tan{\beta}}{1\,–\,\tan{\alpha}\tan{\beta}}$
Thus, you can write tan of angle sum identity in terms of any two angles in trigonometry.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved