Pure surd

Definition

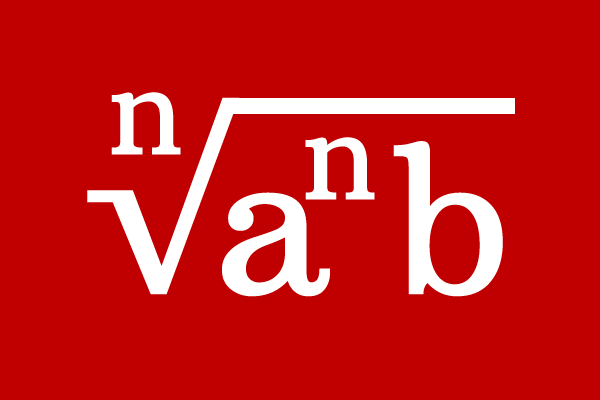
A surd of represents the entire quantity under the root symbol is called an entire surd.

The part of the multiplying factor of a quantity under the root can be taken out from the root in some cases but the entire number is displayed under the root. Hence, the surd is known as an entire surd. The entire surd is purely a surd. For this reason, the entire surd is also called as a pure surd.

Example

$(1)\,\,\,\,\,\,$ $\sqrt{8}$

Express the number $8$ as multiplying factors of $2$.
$\implies \sqrt{8} = \sqrt{2 \times 2 \times 2} = \sqrt{2^2 \times 2}$
$\implies \sqrt{8} = \sqrt{2^2} \times \sqrt{2}$
$\implies \sqrt{8} = 2 \sqrt{2}$

In this example, $\sqrt{8}$ can be expressed as $2\sqrt{2}$ but it is expressed purely as a surd by displaying it as $\sqrt{8}$. Hence, the surd $\sqrt{8}$ is called as an entire surd or pure surd in mathematics.

$(2)\,\,\,\,\,\,$ $\sqrt[\displaystyle 3]{81}$

$(3)\,\,\,\,\,\,$ $\sqrt[\displaystyle 4]{343}$

$(4)\,\,\,\,\,\,$ $\sqrt[\displaystyle 5]{78125}$

$(5)\,\,\,\,\,\,$ $\sqrt[\displaystyle 6]{9765625}$

If any surd contains no multiplying factor outside the root, call the surd as an entire surd or pure surd.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.