$\sec{\theta} \,=\, \dfrac{1}{\cos{\theta}}$
Cosine is a ratio of lengths of adjacent side to hypotenuse and the secant is a ratio of lengths of hypotenuse to adjacent side. The cosine and secant functions are mutually reciprocals. Therefore, the reciprocal of cos of angle equals to secant of angle.
$\Delta QPR$ is a right triangle and its angle is theta ($\theta$).
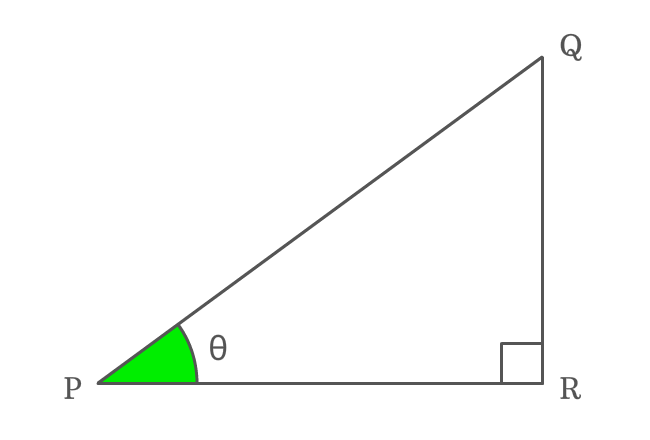
First of all, write cos of angle theta ($\cos{\theta}$) in its ratio form.
$\cos{\theta} \,=\, \dfrac{PR}{PQ}$
In the same way, write the secant of angle theta ($\sec{\theta}$) in its ratio form.
$\sec{\theta} \,=\, \dfrac{PQ}{PR}$
Now, write the value of secant function in ratio form into its reciprocal form mathematically. It helps us to identity the relation between cosine and secant functions.
$\implies \sec{\theta} \,=\, \dfrac{1}{\dfrac{PR}{PQ}}$
$\,\,\, \therefore \,\,\,\,\,\,$ $\sec{\theta} \,=\, \dfrac{1}{\cos{\theta}}$
Therefore, it has proved that the reciprocal of cos function is equal to secant function. It is used as a trigonometric formula in mathematics.
Any symbol can be used to represent angle of right triangle but the reciprocal identity of cos function should be written in terms of corresponding angle.
For example, if angle of right triangle is denoted by $x$, then
$\sec{x} \,=\, \dfrac{1}{\cos{x}}$
Similarly, if angle of right triangle is represented by $A$, then
$\sec{A} \,=\, \dfrac{1}{\cos{A}}$
The reciprocal identity of cos function is written in this form but the only changing factor is angle of the right triangle.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved