A quantity that appears inside the brackets in a matrix is called an entry of a matrix.
A quantity, displayed inside a matrix in a specific row and column is called an element of the matrix.
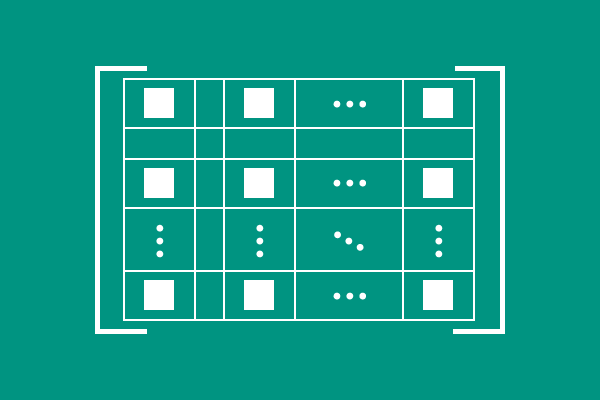
The space inside a matrix is divided as required number of rows and columns on the basis of total number of elements. Every element is displayed in specific row and column but every two elements in a row or column are separated by some space.
$3$, $6$, $-7$, $8$, $0$ and $4$ are elements in the following example matrix.
$\begin{bmatrix}
3 & 6 & -7 \\
8 & 0 & 4 \\
\end{bmatrix}$
There is some space between every two elements in each row and each column for displaying them clearly in a matrix.
Every element of a matrix is usually represented by a variable with two subscripts in which first subscript denotes the row of element and the second subscript denotes the column of the same element.
All elements are displayed in a matrix in general form.
$\begin{bmatrix}
e_{11} & e_{12} & e_{13} & \cdots & e_{1n} \\
e_{21} & e_{22} & e_{23} & \cdots & e_{2n} \\
e_{31} & e_{32} & e_{33} & \cdots & e_{3n} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
e_{m1} & e_{m2} & e_{m3} & \cdots & e_{mn} \\
\end{bmatrix}$
In this example, each element is displayed by a variable with two subscripts. The first and second subscripts of the literal represent row and column of the respective element.
A matrix can also be expressed in compact form. In this method, only one element is displayed by a variable with two subscripts but the two subscripts are also denoted by two variables.
If the row and column are denoted by $i$ and $j$ respectively, then the matrix is expressed in compact form as follows.
$\begin{bmatrix}
e_{ij}
\end{bmatrix}$
The element $e_{ij}$ represents every element in the matrix generally and $i = 1, 2, 3 \ldots$ and $j = 1, 2, 3 \ldots$
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved