Binary Logarithm

A logarithmic system which contains $2$ as its base, is called binary logarithm.

Introduction

Michael Stifel (or Styfel), a German mathematician who studied both natural logarithms and common logarithms and developed Binary Logarithms by taking $2$ as base of the logarithms.

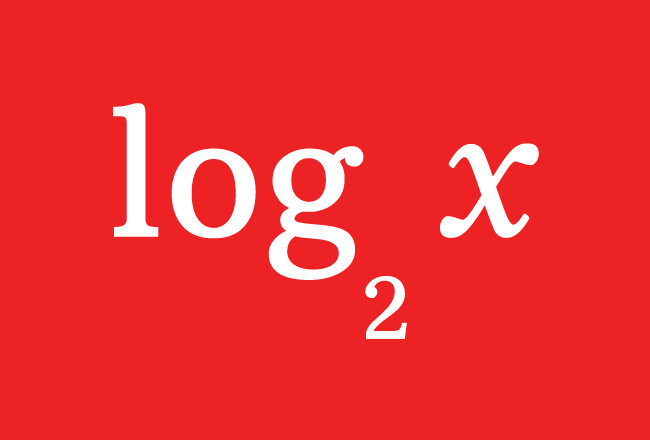
The actual meaning of binary is two pieces or two parts. So, he split the quantities as multiplying factors on the basis of number $2$. Hence, his logarithmic system is called as binary logarithmic system.

It is useful to do calculations like multiplication and division easily.

Algebraic form

Logarithm is represented by $\log$ symbol simply and $2$ is used as subscript of the log to express that $2$ is a base of the logarithm.

Representation

If a quantity is represented by $q$, then logarithm of $q$ to base $2$ is written in mathematics as $\log_{2}{q}$. It is also commonly written as $\operatorname{lb}{q}$.

Therefore, $\log_{2}{q}$ and $\operatorname{lb}{q}$ both represent binary logarithm of quantity $q$ in mathematics.

Inverse Operation

The Binary Logarithm and Exponentiation are inverse operations. So, it is must to learn the relation between them.

It is taken that the total number of multiplying factors is denoted by $x$ when the quantity $q$ is divided as multiplying factors on the basis of quantity $2$.

$\log_{2}{q} \,=\, x$ then $q \,=\, 2^{\displaystyle x}$

Therefore, $\log_{2}{q} \,=\, x$ $\, \Leftrightarrow \,$ $q \,=\, 2^{\displaystyle x}$

It can also be expressed as

$\operatorname{lb}{q} \,=\, x$ $\, \Leftrightarrow \,$ $q \,=\, 2^{\displaystyle x}$