A triangle which contains right angle as one of its three angles is called right triangle (or) right angled triangle.
The meaning of right triangle is defined by combining the meanings of right angle and triangle. A right angle represents $90$ degrees. So, if any triangle contains right angle as one of its interior angles, then the triangle is called as right angled triangle or simply called as right triangle in geometric mathematics.
In a right triangle, there are three interior angles in which one of them is a right angle and other two angles are complementary angles.
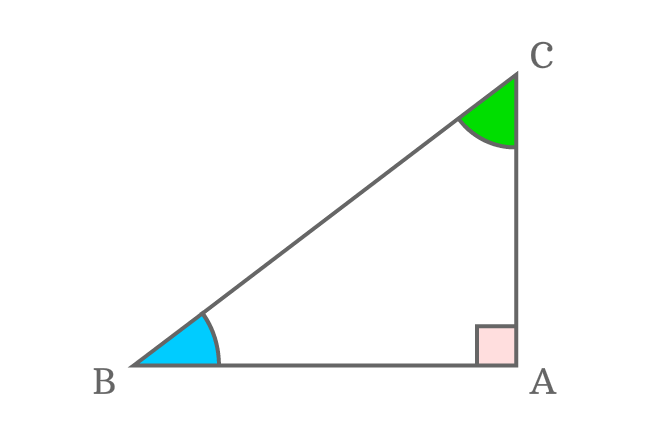
The angle between opposite side (perpendicular) and adjacent side (base) is a right angle.
$\angle BAC$ is right angle in this right triangle. So, $\angle BAC = 90^\circ$.
The angle between adjacent side (base) and hypotenuse is called angle of right triangle. It is quite opposite to the opposite side of the triangle.
In this example, $\angle ABC$ is angle of right triangle.
There is an angle between hypotenuse and opposite side (perpendicular). It is $\angle BCA$ and also a complementary angle of angle of right triangle. So, it can be calculated by using formula of complementary angles.
$\angle BCA = 90^\circ-\angle ABC$
The right triangle is a special triangle. So, each side of this type of triangle is called by a special name.
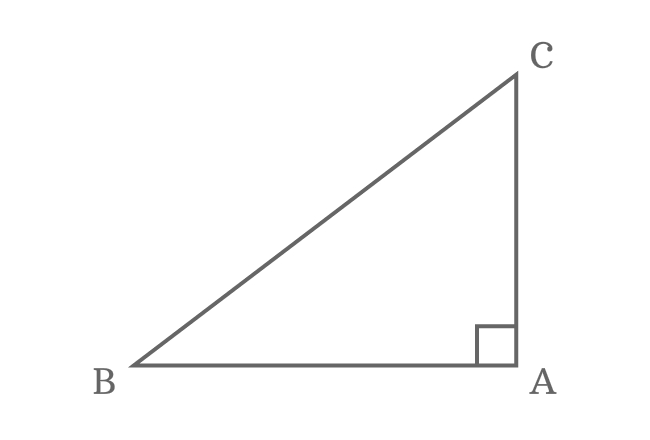
A side which acts as a base of the triangle is called adjacent side and it is also called as base.
A side which makes a right angle with adjacent side is called opposite side.
A side that joins end points of both opposite and adjacent sides is called hypotenuse.
The right triangle has some geometric properties naturally. So, everyone must have to know them to study the geometry in advanced level.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved