The sum of all three interior angles in a triangle is $180^\circ$.
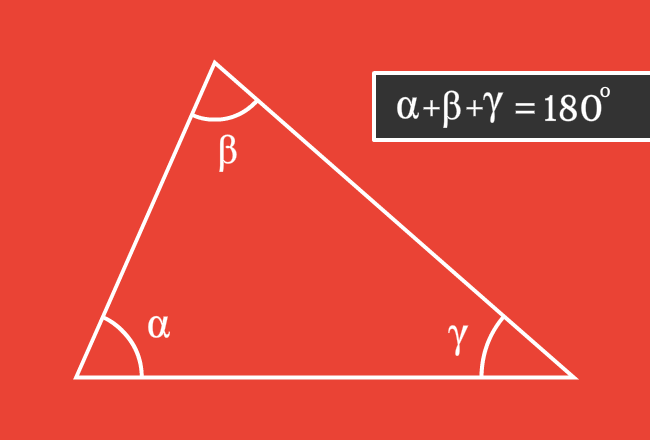
Three interior angles are formed internally by the intersection of every two sides of a triangle. The addition of all three angles is always equal to $180^\circ$ geometrically.
If, $\alpha$, $\beta$ and $\gamma$ are three interior angles in a triangle, then
$\alpha+\beta+\gamma = 180^\circ$
This basic geometrical property of a triangle is often used as a formula in geometry in some special cases
There are three geometrical steps involved for proving that the sum of interior angles in a triangle is equal to $180^\circ$.
$\Delta RST$ is a triangle and its angles are $\alpha$, $\beta$ and $\gamma$.
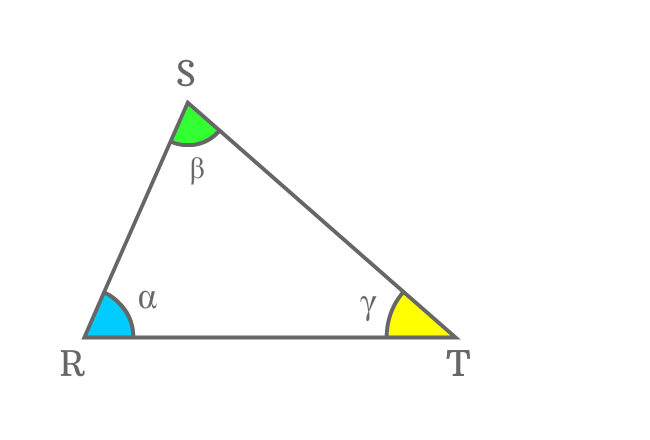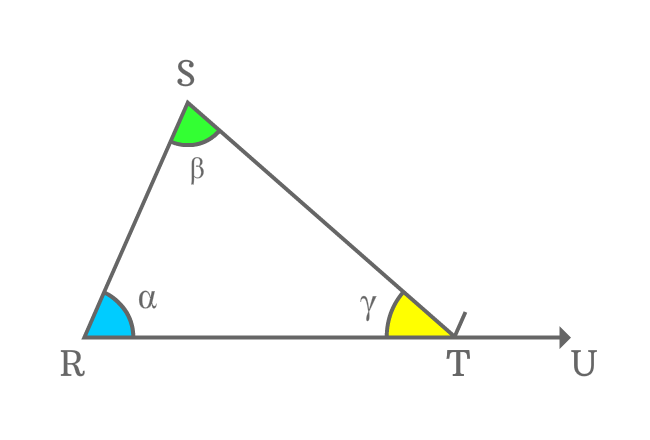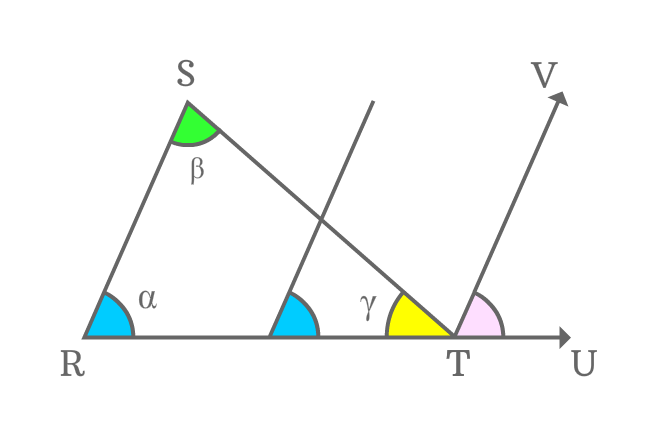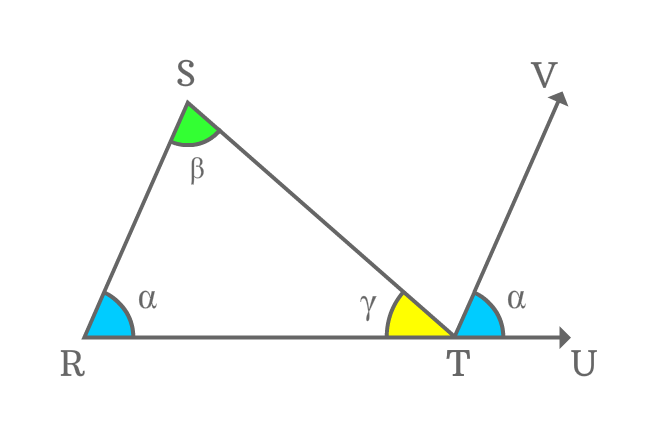
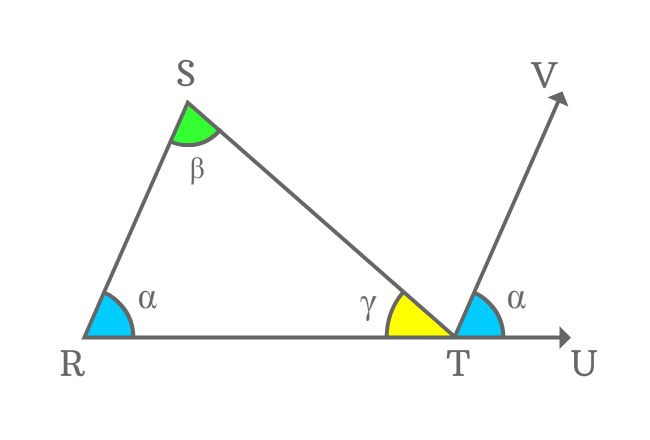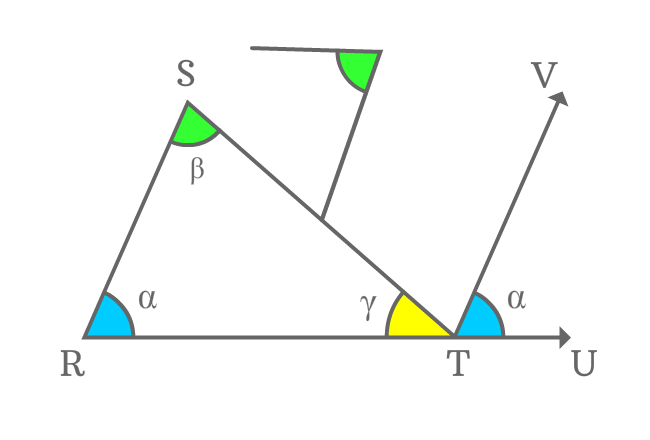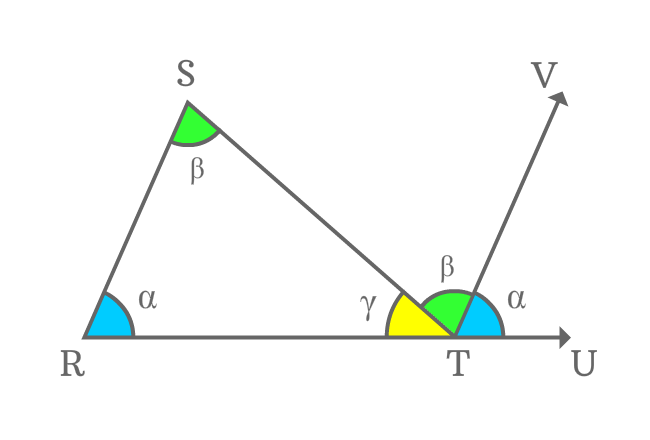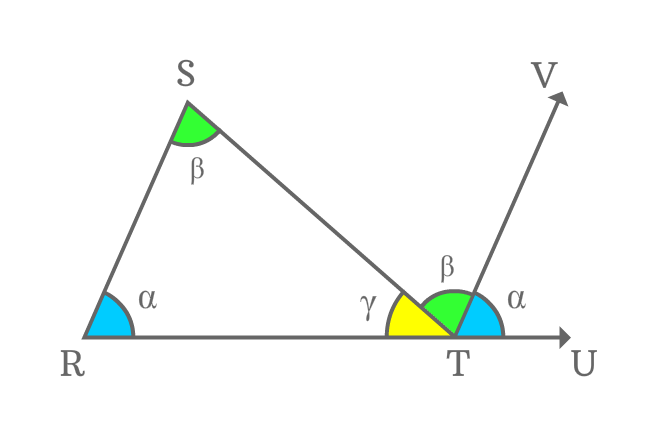
The side $\small \overline{ST}$ is another transversal of the parallel lines $\small \overline{SR}$ and $\small \overline{TV}$. In this case, $\small \angle RST$ and $\small \angle STV$ are interior alternate angles.
It is proved that when two parallel lines are intersected by their transversal, the interior alternate angles are equal.
$\small \angle RST = \angle STV = \beta$
Therefore, $\small \angle STV$ is also equal to $\beta$ geometrically.
$\small \angle RTS$, $\small \angle STV$ and $\small \angle VTU$ are three angles and sum of three interior angles is equal to $\small \angle RTU$.
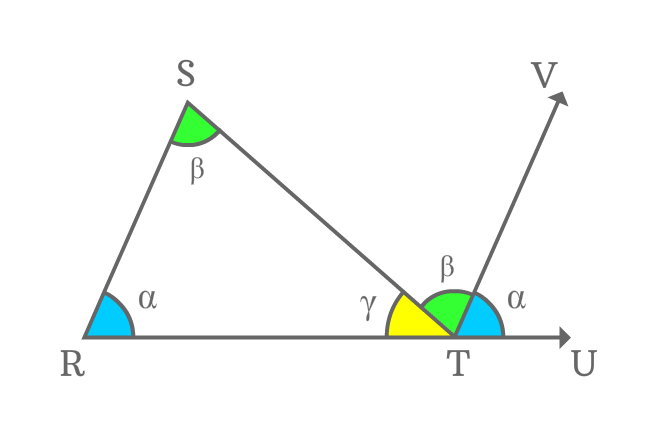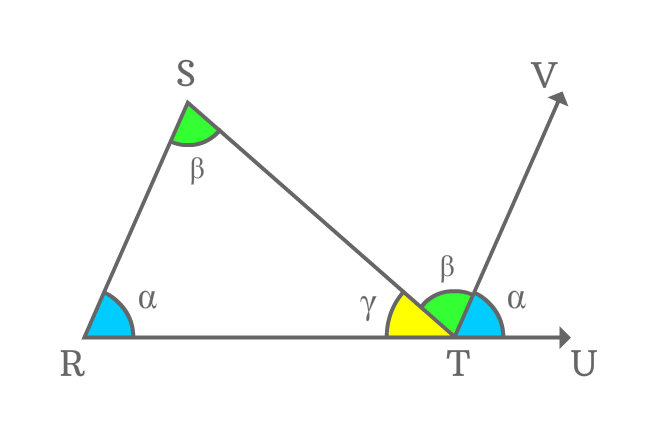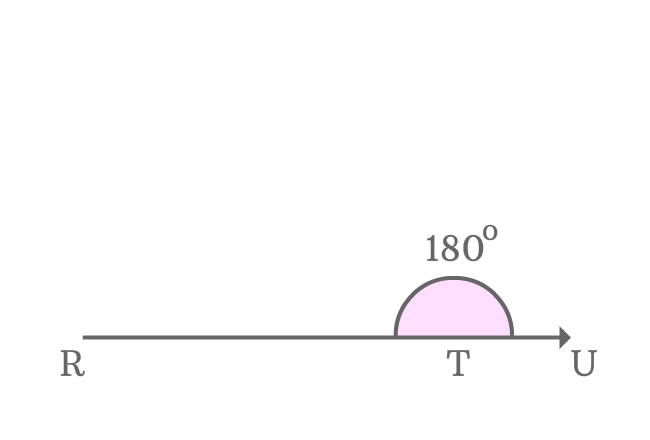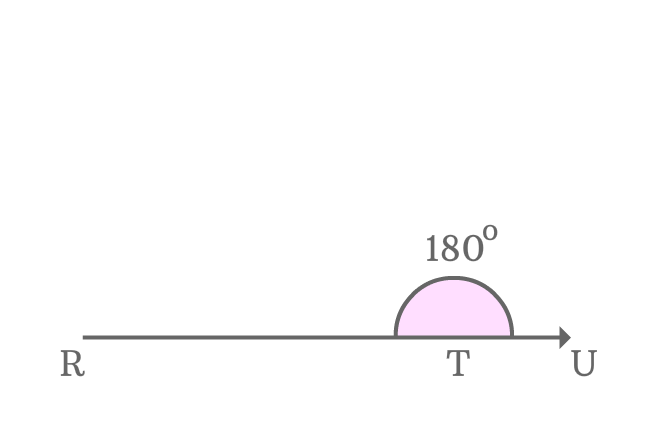
$\small \angle RTS + \angle STV + \angle VTU$ $\,=\,$ $\small \angle RTU$
Actually, $\small \angle RTU$ is a straight angle of the straight line $\small \overline{RU}$. Geometrically, the angle of a straight line is equal to $180^\circ$.
$\implies$ $\small \angle RTS + \angle STV + \angle VTU$ $\,=\,$ $\small \angle RTU$ $\,=\,$ $180^\circ$
$\implies$ $\gamma+\beta+\alpha$ $\,=\,$ $180^\circ$
$\,\,\, \therefore \,\,\,\,\,\, \alpha+\beta+\gamma \,=\, 180^\circ$
$\alpha$, $\beta$ and $\gamma$ are three interior angles of triangle $RST$ and it is proved that the sum of angles in a triangle is equal to $180^\circ$ geometrically.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved