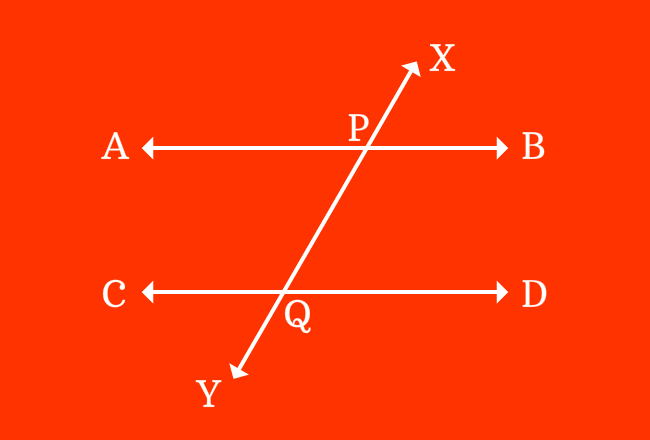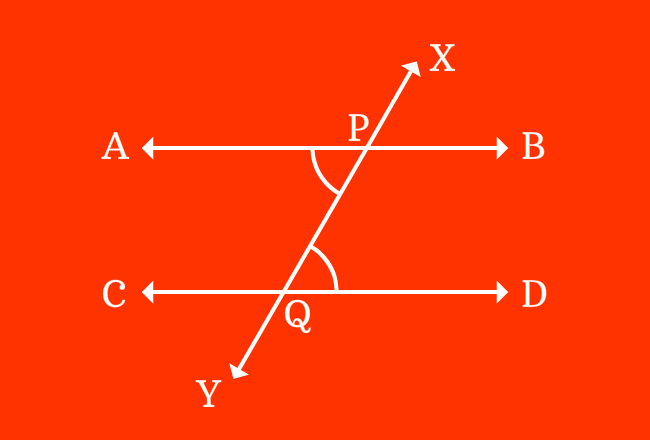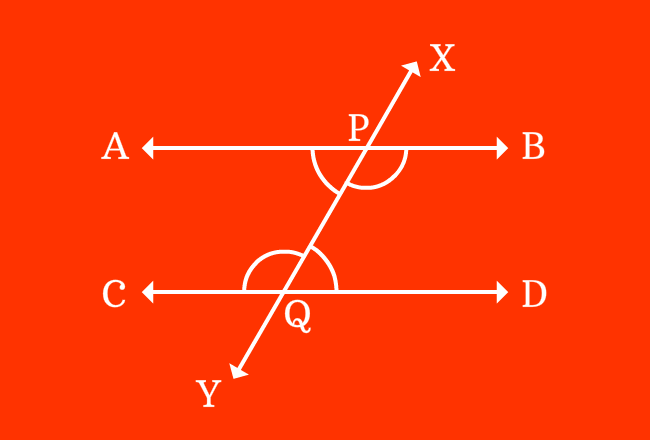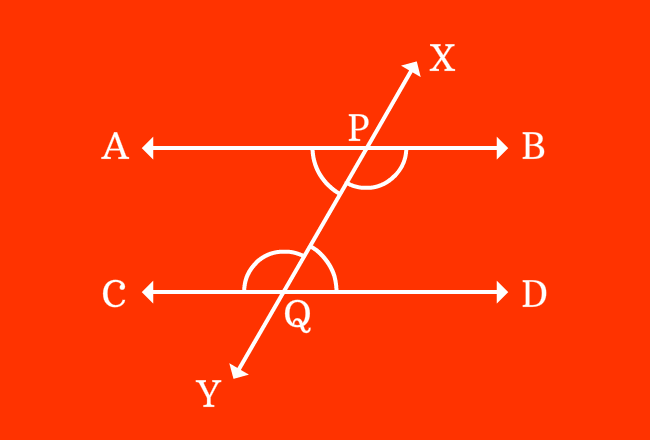
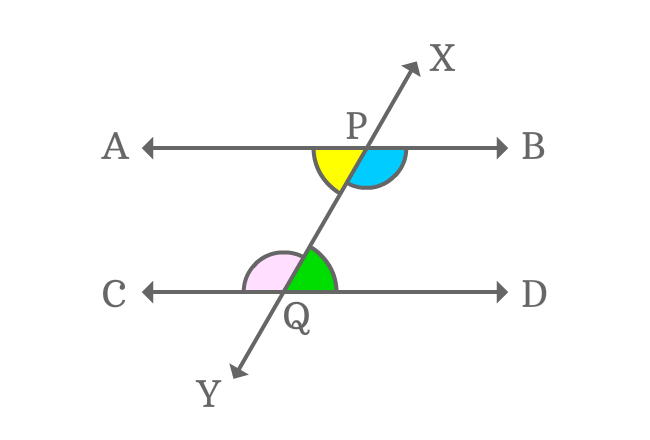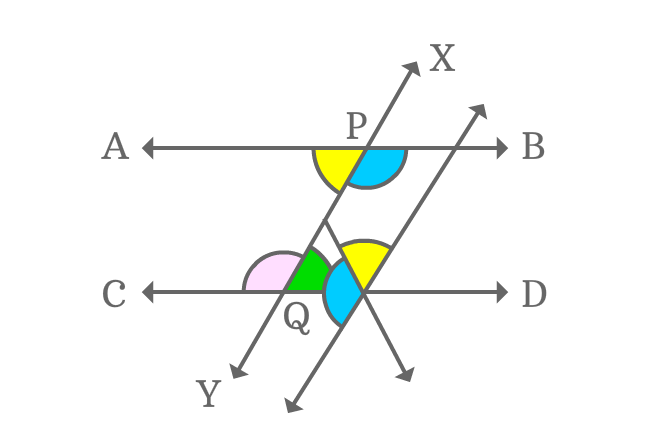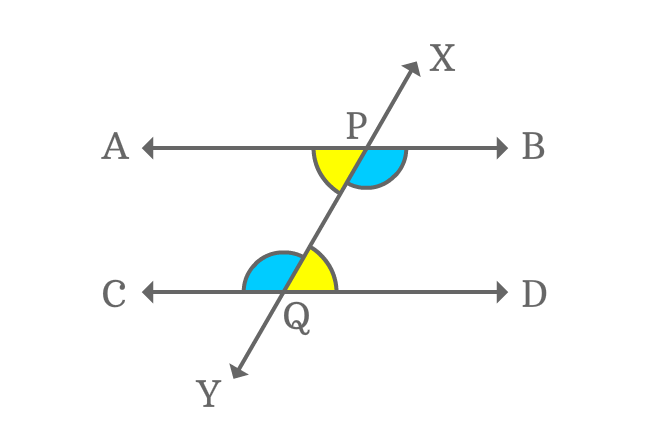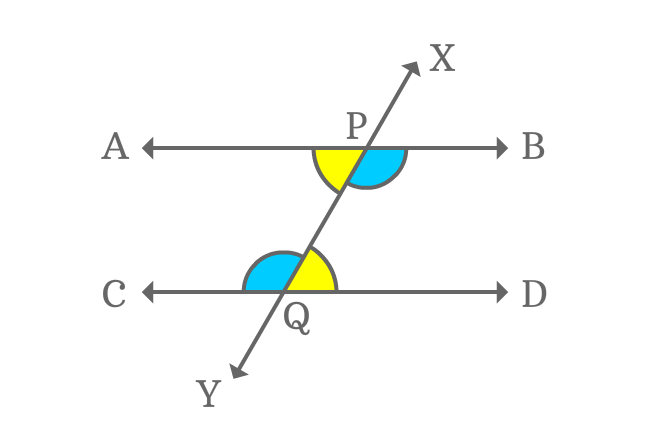
The interior angles which appear opposite sides of transversal of parallel lines are called alternate interior angles formed by parallel lines and their transversal.
When two parallel lines are cut by a transversal, four interior angles are formed geometrically and every two interior angles are appeared oppositely at the intersection of the parallel lines by their transversal.
Thus, two pairs of alternate interior angles are formed when two parallel lines are intersected by their transversal.
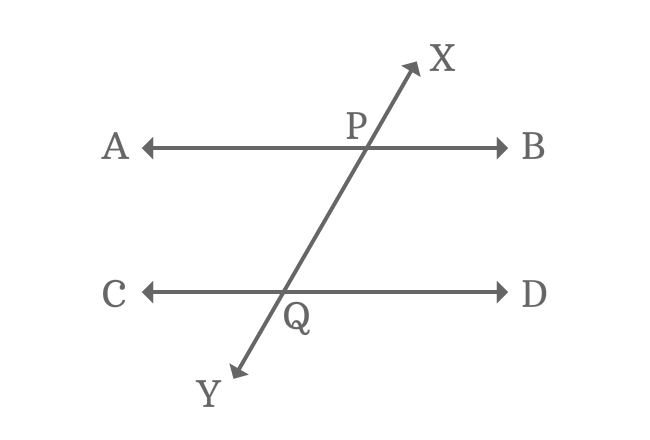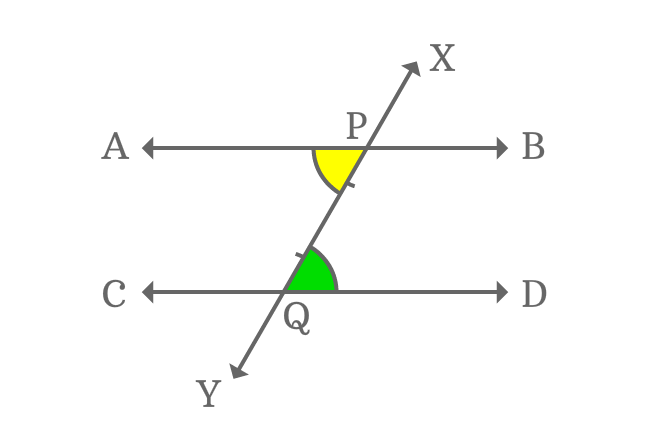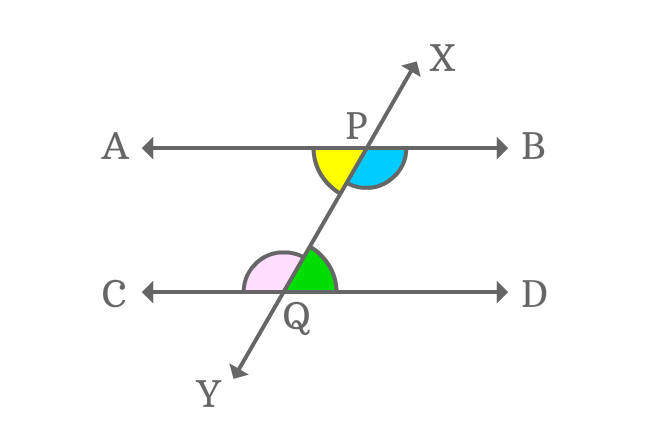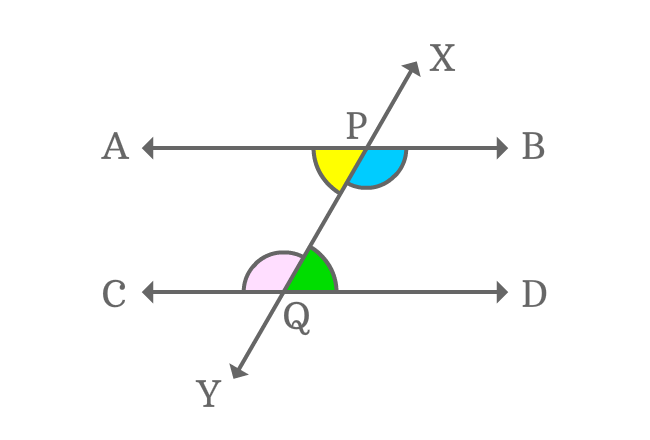
$\angle APY$, $\angle BPY$, $\angle CQX$ and $\angle DQX$ are four interior angles, which are actually formed by the intersection of two parallel lines ($\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$) by their transversal line $\overleftrightarrow{XY}$.
$1. \,\,\,\,\,\,$ $\angle APY$ and $\angle DQX$
$2. \,\,\,\,\,\,$ $\angle BPY$ and $\angle CQX$
The above two pairs of angles are interior angles and also appear opposite sides of the transversal. Therefore, they are called alternate interior angles.
The every pair of alternate interior angles are equal geometrically when two parallel lines are intersected by their transversal line. It is possible because of the parallelism of the parallel lines.
$1. \,\,\,\,\,\,$ $\angle APY \,=\, \angle DQX$
$2. \,\,\,\,\,\,$ $\angle BPY \,=\, \angle CQX$
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved