The formation of an angle by rotating a straight line with a fixed endpoint on a plane is called the formation of an angle by rotation.
Geometrically, an angle is formed, when a straight line with a fixed endpoint is rotated to another position from its initial position on a plane. So, it is called the formation of an angle by rotation.
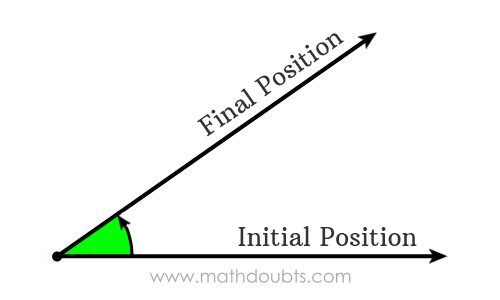
It is a fundamental geometric theory to explain the formation of an angle by rotating a straight line. Now, let’s learn how an angle is formed by rotation from an understandable graphical animation.
Firstly, let’s draw a geometric figure by the below steps.
The ray $\overrightarrow{OP}$ becomes $\overrightarrow{OQ}$ when the ray $\overrightarrow{OP}$ is rotated from its initial position. Now, an $angle \, POQ$ is formed between the rays $\overrightarrow{OP}$ and $\overrightarrow{OQ}$.

In this way, an angle Is formed geometrically, when a straight line is rotated to a position from its initial position. There is also another theory to know the formation of an angle. Now, let’s learn how an angle is formed between two lines.
The geometric formation of angle between straight lines, when two straight lines meet at a point on a plane.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved