A quantity that splits another quantity as its factors is called the base.
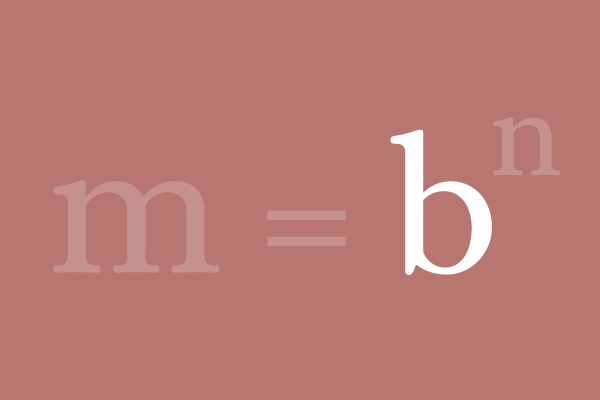
A quantity can be expressed in product form on the basis of another quantity and the product form expression can be written simply in exponential notation as per exponentiation. The quantity that is considered to split a quantity as a product of its terms is called the base of exponential form.
$81$ is a number and express it in product form on the basis of another number $3$ by factorization.
$81 \,=\, 3 \times 3 \times 3 \times 3$
According to exponentiation, write the product form expression in exponential notation.
$81 \,=\, 3^4$
On the basis of number $3$, the number $81$ is expressed as factors of $3$. Hence, the number $3$ is called the base of the exponential notation for the number $81$.
Observe the following examples to understand what exactly the base is in exponential notation.
$(1)\,\,\,\,\,\,\,$ $8 = 2 \times 2 \times 2 = 2^3$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$ In this example, $2$ is the base of the exponential term.
$(2)\,\,\,\,\,\,\,$ $16 = 4 \times 4 = 4^2$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$ In this example, $4$ is the base of the exponential term.
$(3)\,\,\,\,\,\,\,$ $3125 = 5 \times 5 \times 5 \times 5 \times 5 = 5^5$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$ In this example, $5$ is the base of the exponential term.
$(4)\,\,\,\,\,\,\,$ $343 = 7 \times 7 \times 7 = 7^3$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$ In this example, $7$ is the base of the exponential term.
$(5)\,\,\,\,\,\,\,$ $28561 = 13 \times 13 \times 13 \times 13 = 13^4$
$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$ In this example, $13$ is the base of the exponential term.
$m$ is literal and it represents a quantity. Take, the quantity $m$ is divided as factors on the basis of the quantity $b$. The total number of factors of $b$ is $n$ by the factorisation.
$m$ $\,=\,$ $\underbrace{b \times b \times b \times … \times b}_{\displaystyle n factors}$ $\,=\,$ $b^n$
Therefore, the number $b$ is called the base of the exponential notation $b^n$.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved