The expansion of a minus b whole squared algebraic identity can be derived in algebraic form by the geometrical approach. The concept of areas of geometrical shapes such as squares and rectangles are used for proving the a minus b whole square formula in algebraic form.

Take a square and assume the length of each side of this square is represented by $a$.
We have to calculate the area of this geometric shape mathematically. According to the mathematics, the area of a square is equal to the square of the length of the side.
In this case, it is taken that the length of the each side is equal to $a$. Therefore, the area of this square is equal to $a^2$, which is very important to remember for deriving the $a-b$ whole square algebraic identity.
For proving the $a$ minus $b$ whole squared formula geometrically, we have to split the square as four different geometrical figures.
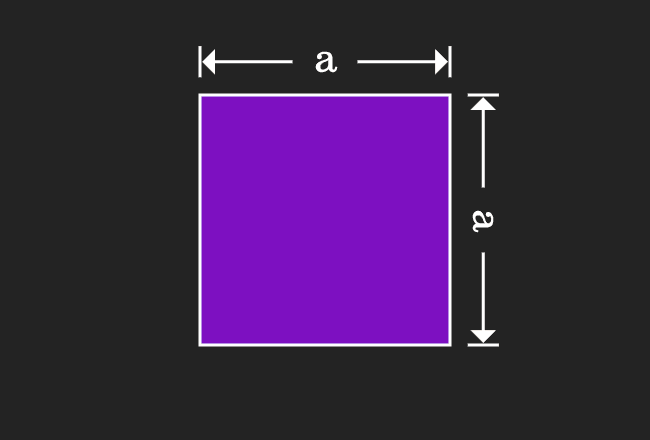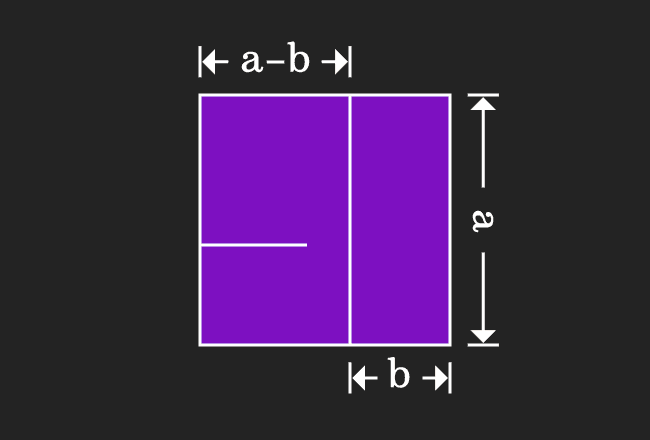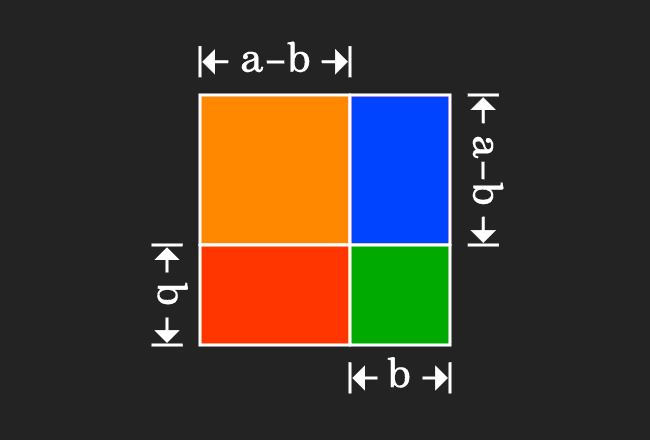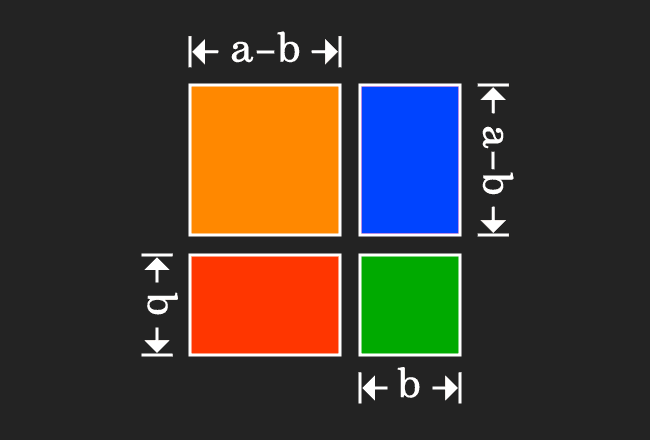
Geometrically, we have successfully divided a square as two small squares and two rectangles.
Now, calculate the area of each geometrical shape mathematically.
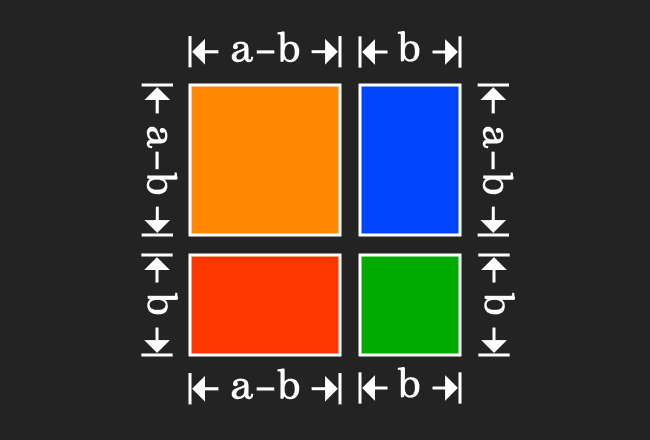
Thus, the areas of all geometrical shapes are calculated and expressed in algebraic form.
It is time to prove the expansion of the $a$ minus $b$ whole squared formula geometrically.
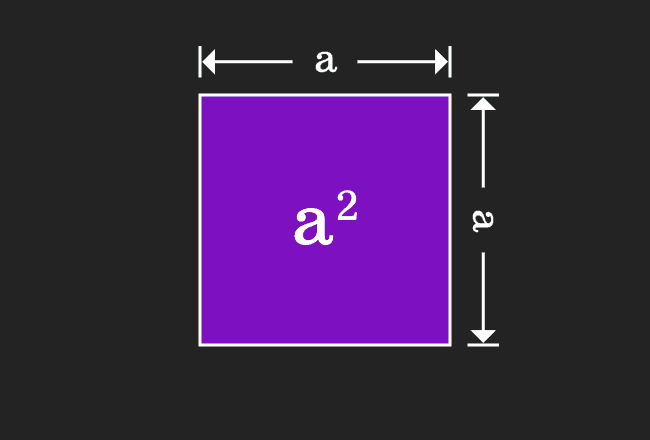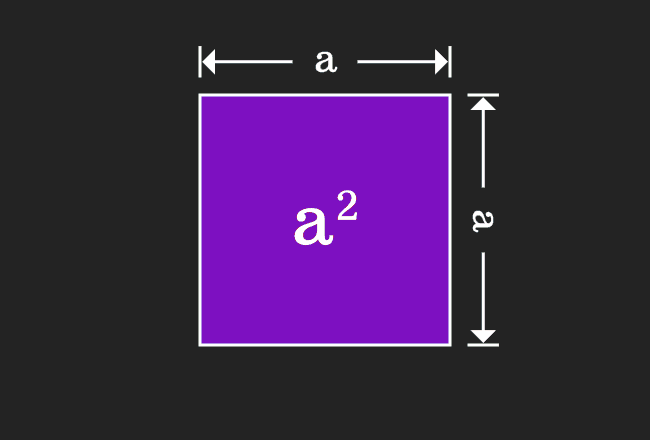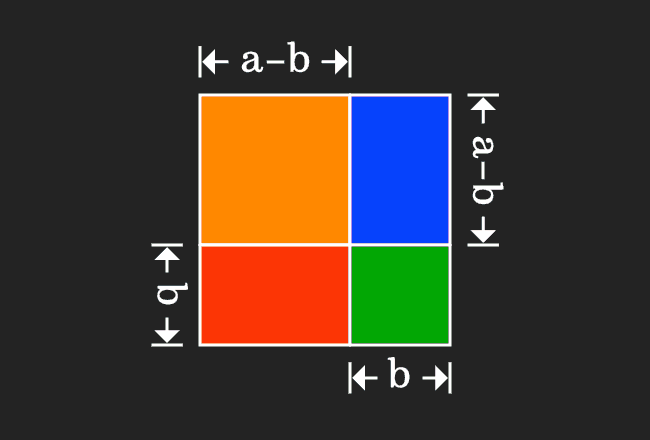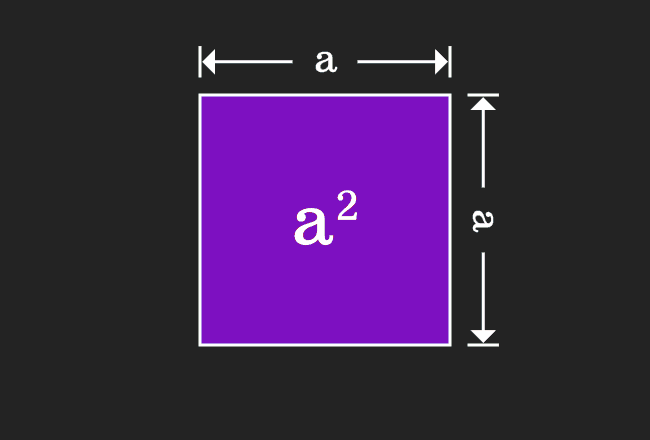
Geometrically, a square is divided as four different geometrical shapes. So, the area of the square is equal to the sum of the areas of the four geometrical shapes. It can be written in mathematical form as an equation.
$a^2$ $\,=\,$ $(a-b)^2$ $+$ $b(a-b)$ $+$ $(a-b)b$ $+$ $b^2$
In this derivation, we have to find the expansion of $(a-b)^2$ identity. So, shift all the terms to other side of the equation for finding the equivalent value of the $a-b$ whole squared.
$\implies$ $a^2$ $-$ $b(a-b)$ $-$ $(a-b)b$ $-$ $b^2$ $\,=\,$ $(a-b)^2$
$\implies$ $(a-b)^2$ $\,=\,$ $a^2$ $-$ $b(a-b)$ $-$ $(a-b)b$ $-$ $b^2$
In the right hand side of the equation, the second and third terms $b(a-b)$ and $(a-b)b$ are equal mathematically as per commutative property of multiplication.
$\implies$ $(a-b)^2$ $\,=\,$ $a^2$ $-$ $b(a-b)$ $-$ $b(a-b)$ $-$ $b^2$
$\implies$ $(a-b)^2$ $\,=\,$ $a^2-2b(a-b)-b^2$
$\implies$ $(a-b)^2$ $\,=\,$ $a^2-2ba+2b^2-b^2$
$\,\,\, \therefore \,\,\,\,\,\,$ $(a-b)^2$ $\,=\,$ $a^2-2ab+b^2$
It is also written as $(a-b)^2$ $\,=\,$ $a^2+b^2-2ab$
It is read as the $a$ minus $b$ whole squared is equal to $a$ squared plus $b$ squared minus $2$ times product of $a$ and $b$. Thus, the $a-b$ whole square algebraic identity is proved in algebraic form geometrically.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved