Proof of a² – b² formula in Geometric Method

Formula

$a^2-b^2 \,=\, (a+b)(a-b)$

The $a^2-b^2$ identity represents the difference of two square quantities and it can be written in factoring form as the product of binomials $a+b$ and $a-b$. The factoring form of $a^2-b^2$ formula can be derived in mathematics geometrically on the basis of areas of geometric shapes.

Subtracting areas of squares

1. Take a square, whose length of each side is $a$ units. Therefore, the area of the square is $a^2$.
2. Draw a small square with the side of $b$ units at any corner of the square. So, the area of small square is $b^2$.
3. Now, subtract the square, whose area is $b^2$ from the square, whose area is $a^2$. It forms a new geometric shape and its area is equal to $a^2-b^2$.

Dividing Area of New shape

1. Divide the new subtracted geometric shape as two different rectangles but the length of one of the two rectangles should be equal to $b$ units.
2. Look at the upper rectangle. Geometrically, the length of this rectangle is $a$ units and its width is $a-b$ units.
3. Similarly, look at the lower rectangle. The length of this rectangle is $a-b$ units and its width is equal to $b$ units.

Difference of Squares in factoring form

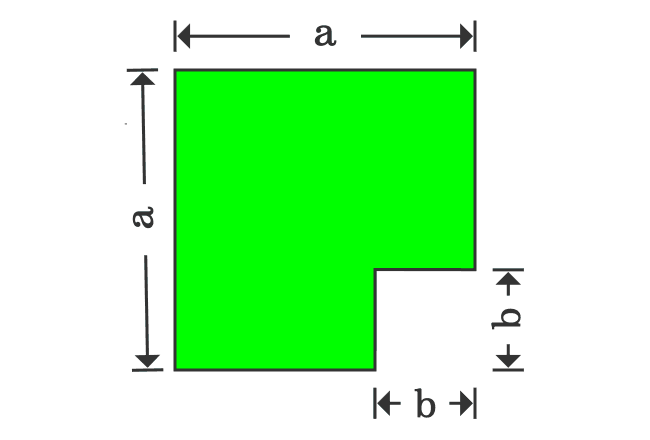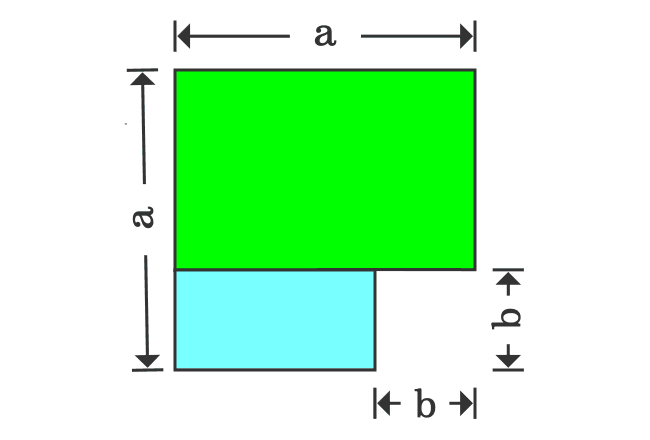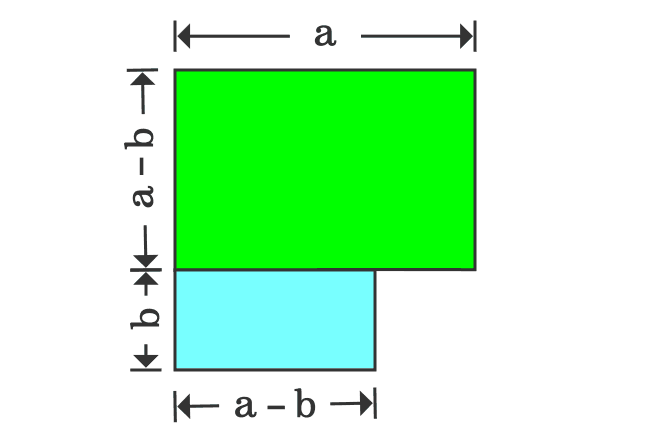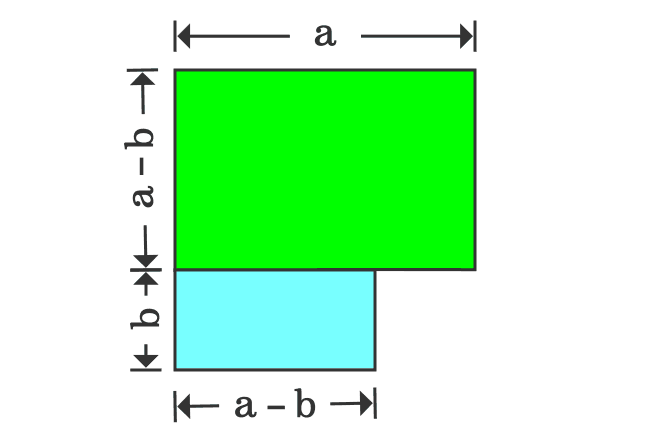
The width of the upper rectangle is $a-b$ and the length of the lower rectangle is also $a-b$ geometrically. If the lower rectangle is rotated by $90^\circ$, then the widths of both rectangles become same and it is useful to join them together as a rectangle.

1. Separate both rectangles.
2. Rotate the lower rectangle by $90^\circ$ and then join both rectangles. It formed another rectangle.
3. The length and width of the new rectangle are $a+b$ and $a-b$ respectively. Therefore, the area of this rectangle is $(a+b)(a-b)$.

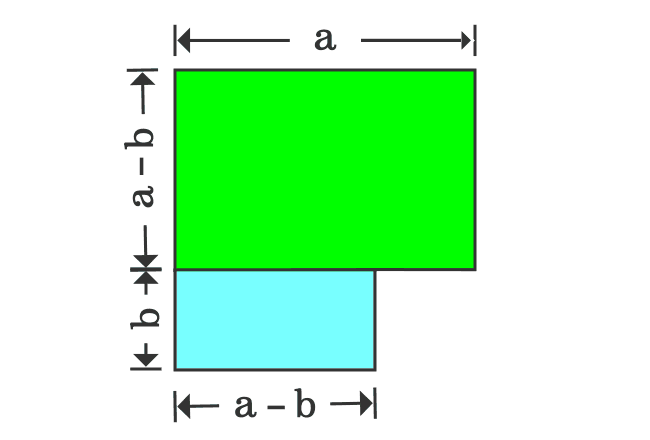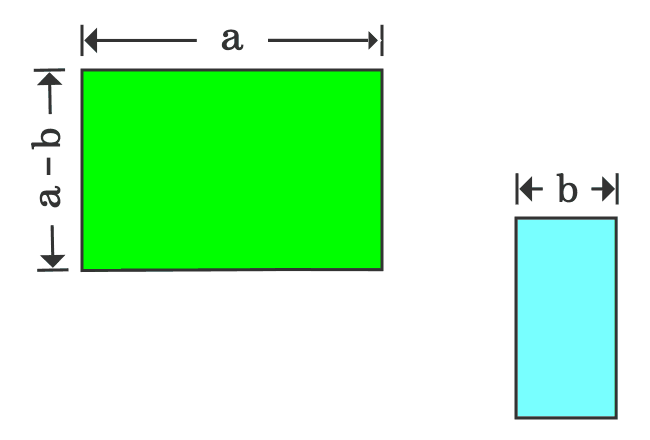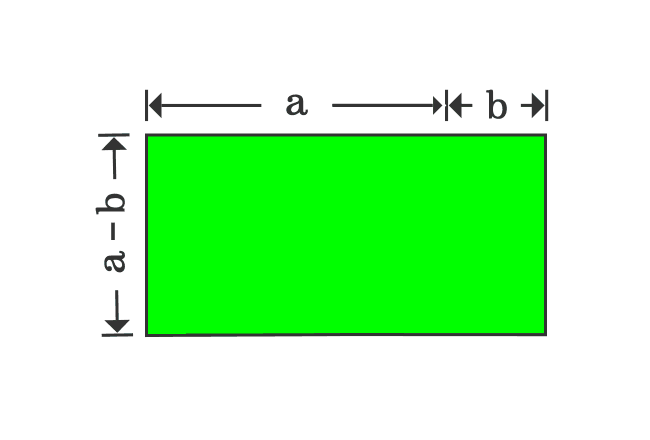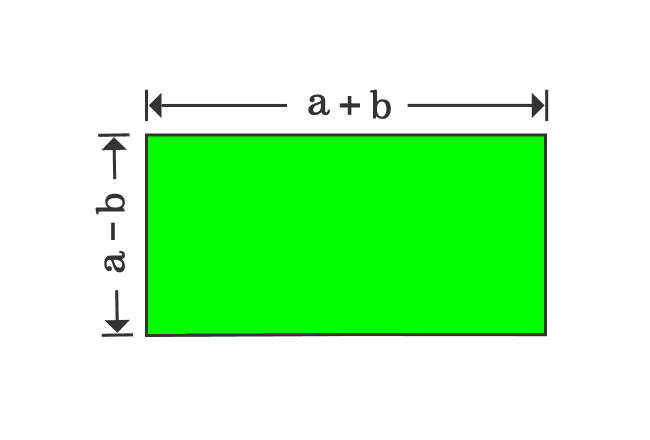
In first step, it is derived that the area of subtracted shape is $a^2-b^2$ and the same shape is now transformed as a rectangle, whose area is ${(a+b)}{(a-b)}$.

Therefore, the areas of both shapes should be equal geometrically.

$\,\,\, \therefore \,\,\,\,\,\, a^2-b^2 \,=\, (a+b)(a-b)$

Geometrically, it is proved that the $a^2$ subtracted $b^2$ is equal to the product of the binomials $a+b$ and $a-b$.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.