Base of Logarithm

A quantity which used to express any other quantity as its multiplying factors is called the base of logarithm.

Introduction

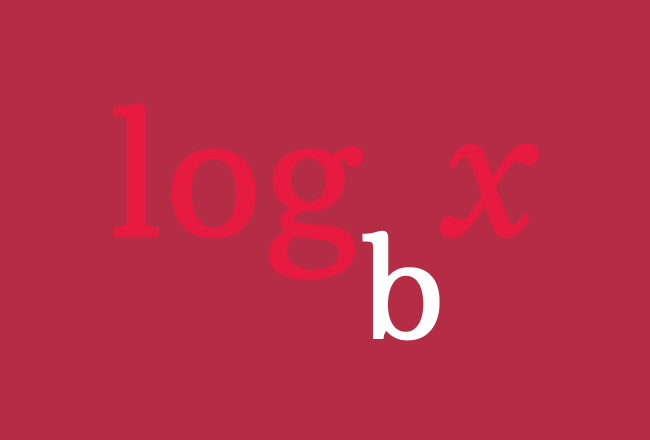
Every quantity can be expressed as multiplying factors of another quantity in mathematics. It can be done by expressing a quantity as multiplying factors on the basis of another quantity.

The relation between the two quantities is represented by a logarithmic symbol $(\log)$ but the quantity which used to transform another number is displayed as subscript of $\log$ symbol for representing that quantity as a base of the mathematical operation.

Example

$256$ is a quantity and let’s try to write this quantity on the basis another quantities to understand the importance of the base of logarithms.

Base 2

$256 = 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2 \times 2$

$\implies 256 = 2^{\displaystyle 8}$

The relationship between three of them is expressed in logarithms.

$\log_{\displaystyle 2} 256 = 8$

On the basis of number $2$, the number $256$ is expressed as eight multiplying factors. Therefore, the number $2$ is called as base of the logarithm of $256$.

Base 4

$256 = 4 \times 4 \times 4 \times 4$

$\implies 256 = 4^{\displaystyle 4}$

Express the relation between three of them in logarithm system.

$\log_{\displaystyle 4} 256 = 4$

On the basis of number $4$, the number $256$ is written as four multiplying factors. Hence, the number $4$ is called as base of the logarithm of $256$.

Base 16

$256 = 16 \times 16$

$\implies 256 = 16^{\displaystyle 2}$

Write relation between three of them in logarithms.

$\log_{\displaystyle 16} 256 = 2$

On the basis of $16$, the number $256$ is expressed as two multiplying factors of $16$. Therefore, the number $16$ is called as base of the logarithm of $256$.

The three cases are the best examples for understanding the concept of base of the logarithms.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.