Collinear points

The three or more points which lie on the same straight line are called collinear points.

Introduction

The meaning of collinear is lying on same straight line. A straight line is usually denoted geometrically by two points and they obviously lie on it. If three or more points are displayed on same straight line, then the points are called collinear points in geometry.

Example

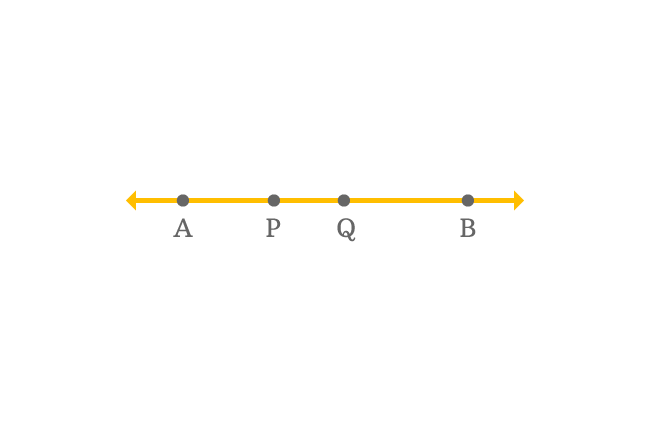
$\overleftrightarrow{AB}$ is a straight line and it is displayed by two points $A$ and $B$ in geometric system.

$P$ and $Q$ are two other points but they lie on the same straight line along with points $A$ and $B$ in the plane.

The total number of points are four in this case and it is more than three. Therefore, the points $A$, $B$, $P$ and $Q$ are called as collinear points in geometry.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.