The angle sum cosine identity is used as a formula to expanded cosine of sum of two angles. For example, $\cos{(A+B)}$, $\cos{(x+y)}$, $\cos{(\alpha+\beta)}$, and so on. Here, you learn how cos of sum of two angles formula is derived in geometric method.
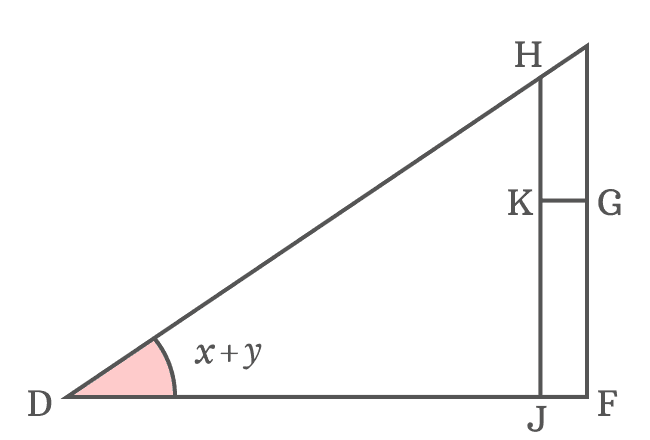
The $\Delta EDF$ is a right triangle and the angle of this triangle is divided as two angles. It’s useful in deriving the cosine of sum of two angles trigonometric identity geometrically.
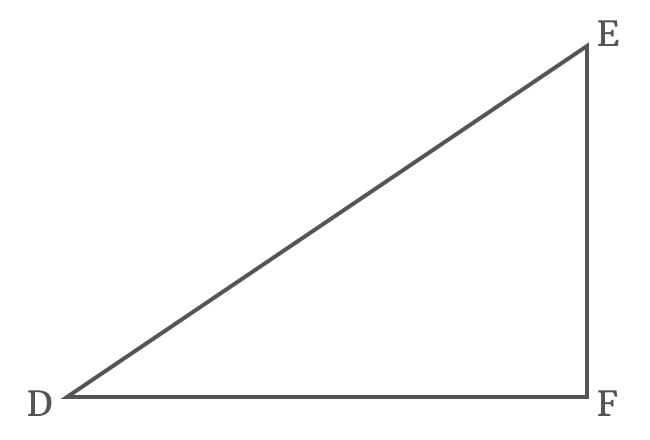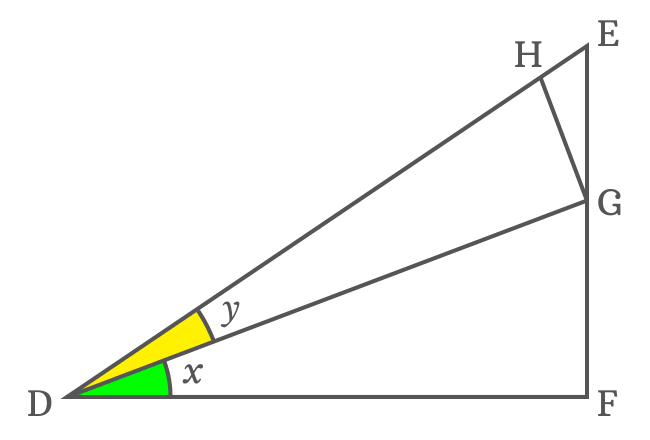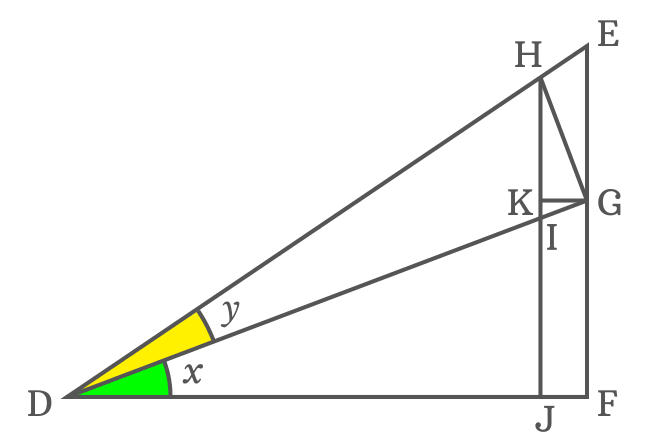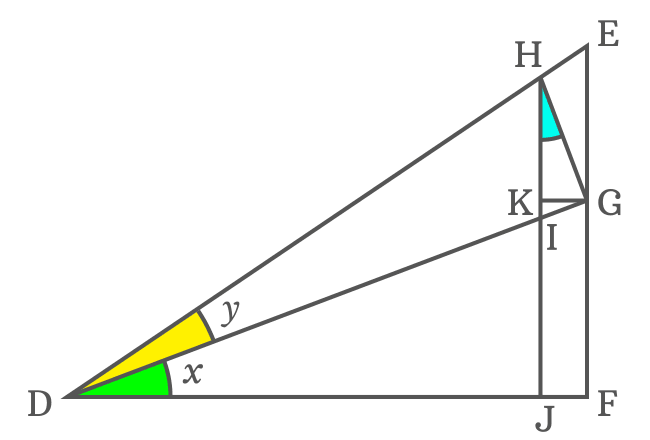
$(1). \,\,\,$ Firstly, draw a straight line to side $\overline{EF}$ from point $D$ for dividing the $\angle EDF$ as two angles $x$ and $y$, and it intersects the side $\overline{EF}$ at point $G$.
$(2). \,\,\,$ Draw a straight line to side $\overline{DE}$ from point $G$ but it should be perpendicular to the side $\overline{DG}$. It means $\overline{DG} \perp \overline{HG}$
$(3). \,\,\,$ Similarly, draw a perpendicular line to side $\overline{DF}$ from point $H$, but it intersects the side $\overline{DG}$ at point $I$ and also perpendicularly intersects the side $\overline{DF}$ at point $J$.
$(4). \,\,\,$ Lastly, draw a perpendicular line to side $\overline{HJ}$ from point $G$ and it intersects the side $\overline{HJ}$ at point $K$.
Thus, the $\Delta GDF$ having $x$ as its angle, the $\angle EDG$ having $y$ as its angle and $\angle KHG$ with unknown angle are formed geometrically.
Now, let’s start the geometrical approach to derive the angle sum cosine identity in the form of $\cos{(x+y)}$ formula in trigonometry on the basis of the above constructed triangle.
The $\angle JDH$ is $x+y$ in the $\Delta JDH$ and write the cos of compound angle $x+y$ in its ratio from.
$\cos{(x+y)}$ $\,=\,$ $\dfrac{DJ}{DH}$
The side $\overline{HJ}$ divides the side $\overline{DF}$ as two parts. So, the sum of lengths of the sides $\overline{DJ}$ and $\overline{JF}$ is equal to the length of the side $\overline{DF}$.
$DF \,=\, DJ+JF$
$\implies DJ \,=\, DF-JF$
Substitute the length of the side $\overline{DJ}$ by its equivalent value in the expansion of $\cos{(x+y)}$.
$\implies$ $\cos{(x+y)}$ $\,=\,$ $\dfrac{DF-JF}{DH}$
$\implies$ $\cos{(x+y)}$ $\,=\,$ $\dfrac{DF}{DH}$ $\,-\,$ $\dfrac{JF}{DH}$
The lengths of sides $\overline{JF}$ and $\overline{KG}$ are equal because they both are parallel lines. Therefore, $JF = KG$
$\implies$ $\cos{(x+y)}$ $\,=\,$ $\dfrac{DF}{DH}$ $\,-\,$ $\dfrac{KG}{DH}$
The side $\overline{DF}$ is adjacent side of $\Delta FDG$ and angle of this triangle is $x$. It is possible to express the length of the side $\overline{DF}$ in a trigonometric function.
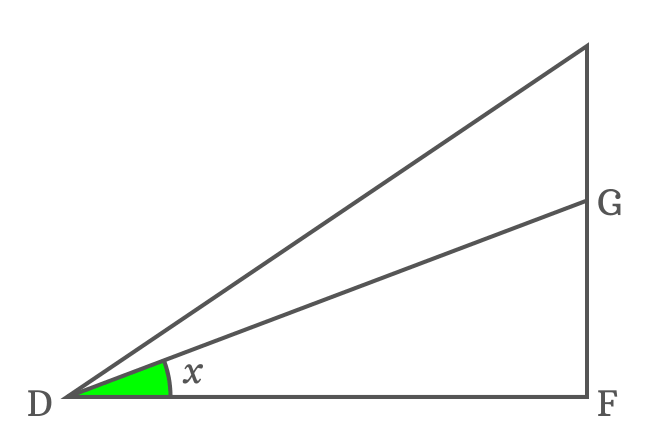
$\cos{x} \,=\, \dfrac{DF}{DG}$
$\implies DF \,=\, {DG}\cos{x}$
Replace the length of the side $\overline{DF}$ by its equivalent value in the $\cos{(x+y)}$ expansion.
$\implies$ $\cos{(x+y)}$ $\,=\,$ $\dfrac{{DG}\cos{x}}{DH}$ $\,-\,$ $\dfrac{KG}{DH}$
$\implies$ $\cos{(x+y)}$ $\,=\,$ $\cos{x} \times \dfrac{DG}{DH}$ $\,-\,$ $\dfrac{KG}{DH}$
$DG$ and $DH$ are lengths of the sides $\overline{DG}$ and $\overline{DH}$ respectively. They are sides of the $\Delta GDH$ and its angle is $y$. The ratio between them can be represented by cos of angle $y$.
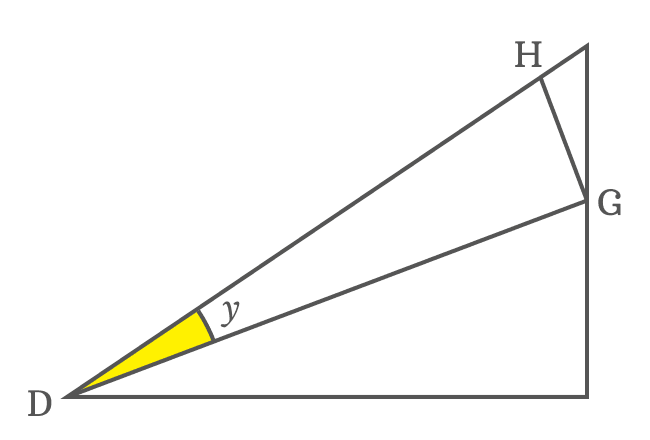
$\cos{y} \,=\, \dfrac{DG}{DH}$
The ratio of $DG$ to $DH$ can be replaced by $\cos{y}$ in the expansion of $\cos{(x+y)}$.
$\implies$ $\cos{(x+y)}$ $\,=\,$ $\cos{x} \times \cos{y}$ $\,-\,$ $\dfrac{KG}{DH}$
$\implies$ $\cos{(x+y)}$ $\,=\,$ $\cos{x}\cos{y}$ $\,-\,$ $\dfrac{KG}{DH}$
Similarly, the ratio of $KG$ to $DH$ can also be expressed in terms of trigonometric functions but it is not possible at this time because it’s the side of the $\Delta KHG$ and its angle is unknown.
Now, it’s time to find the $\angle KHG$ and it is useful to us in expressing the length of the side $\overline{KG}$ in a trigonometric function. The sides $\overline{KG}$ and $\overline{DF}$ are parallel lines and their transversal is $\overline{DG}$. The $\angle FDG$ and $\angle KGD$ are alternate interior angles and they are equal geometrically.
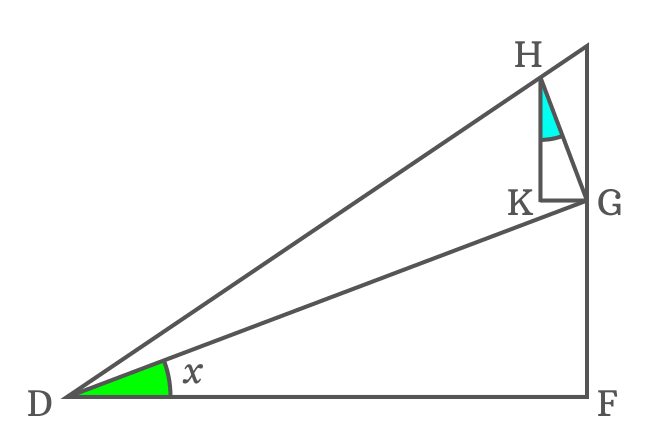
$\angle KGD \,=\, \angle FDG$ but $\angle FDG = x$
$\therefore \,\,\,\,\,\, \angle KGD \,=\, x$
Actually $\overline{DG} \perp \overline{HG}$. So, $\angle DGH = 90^°$. The side $\overline{KG}$ splits the $\angle DGH$ as two angles $\angle KGD$ and $\angle KGH$.
$\angle DGH \,=\, \angle KGD + \angle KGH$
$\implies 90^° = x+\angle KGH$
$\,\,\, \therefore \,\,\,\,\,\, \angle KGH = 90^°-x$
Two angles are known in $\Delta KHG$ and its third angle $\angle KHG$ can be calculated from them by using sum of angles of a triangle rule.
$\angle KHG + \angle HKG + \angle KGH$ $\,=\,$ $180^°$
$\implies$ $\angle KHG + 90^° + 90^°-x$ $\,=\,$ $180^°$
$\implies$ $\angle KHG + 180^°-x$ $\,=\,$ $180^°$
$\implies$ $\angle KHG$ $\,=\,$ $180^°-180^°+x$
$\implies$ $\angle KHG$ $\,=\,$ $\require{cancel} \cancel{180^°}-\cancel{180^°}+x$
$\,\,\, \therefore \,\,\,\,\,\,$ $\angle KHG \,=\, x$
It is derived that $\angle KHG = x$ but the $\angle FDG = x$ and it clears that they both are congruent. Therefore, $\Delta FDG$ and $\Delta KHG$ are similar triangles.
Let’s continue deriving the expansion of the angle sum cosine identity.
$\cos{(x+y)}$ $\,=\,$ $\cos{x}\cos{y}$ $\,-\,$ $\dfrac{KG}{DH}$
$KG$ is length of the side $\overline{KG}$ in $\Delta KHG$ and it can be written in terms of trigonometric function.
$\sin{x} \,=\, \dfrac{KG}{HG}$
$\implies KG \,=\, {HG}\sin{x}$
Therefore, the length of the side $\overline{KG}$ by its equivalent value in the expansion of cos of compound angle.
$\implies$ $\cos{(x+y)}$ $\,=\,$ $\cos{x}\cos{y}$ $\,-\,$ $\dfrac{{HG}\sin{x}}{DH}$
$\implies$ $\cos{(x+y)}$ $\,=\,$ $\cos{x}\cos{y}$ $\,-\,$ $\sin{x} \times \dfrac{HG}{DH}$
$HG$ and $DH$ are lengths of the sides $\overline{HG}$ and $\overline{DH}$ in $\Delta GDH$. The angle of $\Delta GDH$ is $y$. So, the ratio between them can be represented by the trigonometric function $\sin{y}$.

$\sin{y}$ $\,=\,$ $\dfrac{HG}{DH}$
Therefore, the ratio of $HG$ to $DH$ can be replaced by $\sin{y}$ in the expansion of the $\cos{(x+y)}$ function.
$\implies$ $\cos{(x+y)}$ $\,=\,$ $\cos{x}\cos{y}$ $\,-\,$ $\sin{x} \times \sin{y}$
$\,\,\, \therefore \,\,\,\,\,\,$ $\cos{(x+y)}$ $\,=\,$ $\cos{x}\cos{y}$ $\,-\,$ $\sin{x}\sin{y}$
Therefore, it is proved that the cos of sum of two angles can be expanded as the subtraction of product of sines of angles from product of cosines of the angles.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved