$\cos{\theta}\sec{\theta} \,=\, 1$
Mathematically, the cosine and secant functions are reciprocals. So, their product must be equal to one and the product relation between cos and sec functions can also be proved in trigonometry.
$\Delta RPQ$ is a right triangle and its angle is assumed as theta ($\theta$).
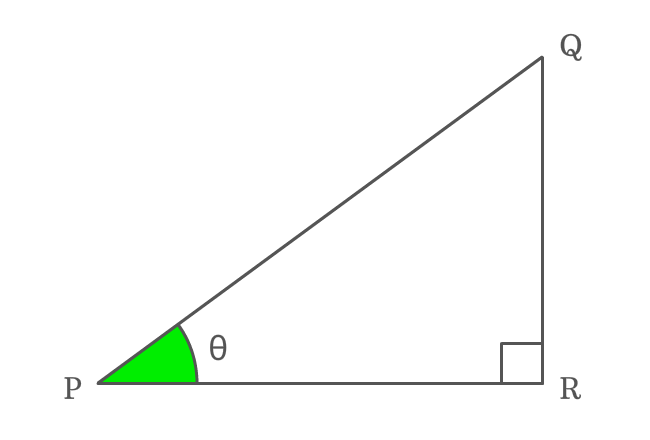
Write cosine function ($\cos{\theta}$) in its ratio form firstly.
$\cos{\theta} \,=\, \dfrac{PR}{PQ}$
Now, write secant function ($\sec{\theta}$) in its ratio form.
$\sec{\theta} \,=\, \dfrac{PQ}{PR}$
Finally, multiply both cosine and secant functions to find the product of them.
$\cos{\theta} \times \sec{\theta}$ $\,=\,$ $\dfrac{PR}{PQ} \times \dfrac{PQ}{PR}$
$\implies$ $\cos{\theta} \times \sec{\theta}$ $\,=\,$ $\dfrac{PR \times PQ}{PQ \times PR}$
$\implies$ $\cos{\theta} \times \sec{\theta}$ $\,=\,$ $\require{cancel} \dfrac{\cancel{PR} \times \cancel{PQ}}{\cancel{PQ} \times \cancel{PR}}$
$\,\,\, \therefore \,\,\,\,\,\,$ $\cos{\theta}.\sec{\theta} \,=\, 1$
Therefore, it has proved that the product of cos and sec functions at an angle is equal one, and this property in trigonometry is used as a formula in mathematics.
Keep one thing in your mind always that the angle of a right triangle can be represented by any symbol but the product of cosine of angle and secant of angle always equals to one.
For example, if $x$ denotes angle of right triangle, then
$\cos{x}.\sec{x} \,=\, 1$
Similarly, if $A$ is used to represent angle of right triangle, then
$\cos{A}.\sec{A} \,=\, 1$
The cosine and secant functions in the trigonometric product identity can be expressed in terms of any angle but the product of them equals to one mathematically.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved