Tan of negative angle

A mathematical relation of tangent of negative angle with tangent of positive angle is called tan of negative angle identity.

Proof

The mathematical relation between tangent of negative angle and tan of positive angle is derived in mathematical form by geometrical method in trigonometry.

Construction of triangle with positive angle

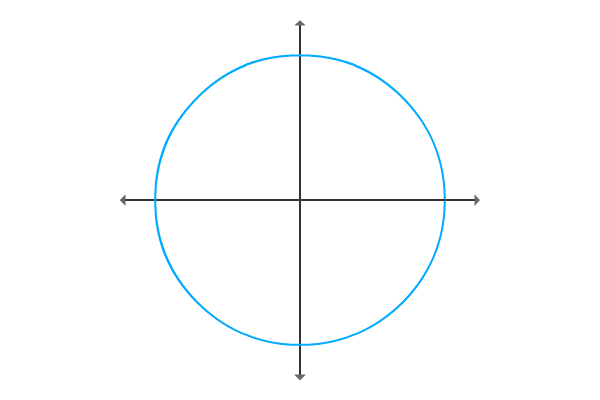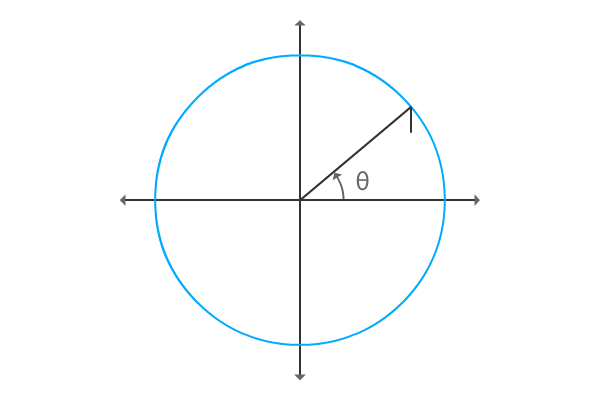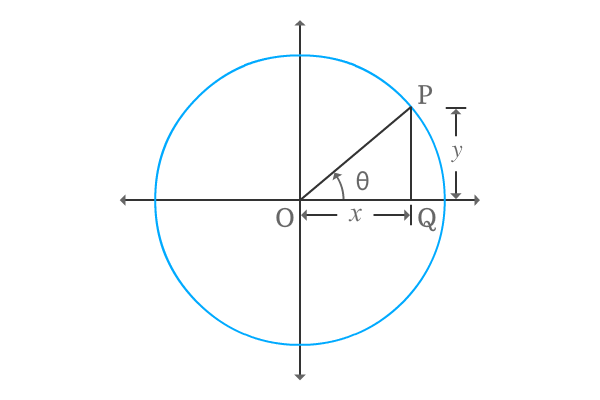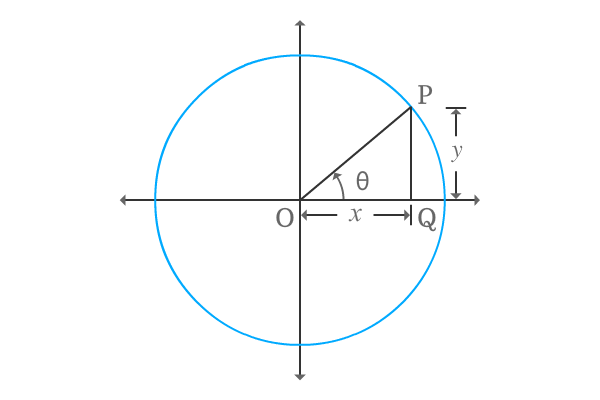
$\Delta POQ$ is a right angled triangle and take its positive angle is denoted by theta. Express tan of positive angle in terms of ratio of lengths of the two respective sides.

$\tan{\theta} \,=\, \dfrac{PQ}{OQ}$

The $\Delta POQ$ is constructed in first quadrant. Therefore, the lengths of both adjacent and opposite sides are positive and take they both are represented by $x$ and $y$ respectively.

$\implies$ $\tan{\theta} \,=\, \dfrac{y}{x}$

Construction of triangle with negative angle

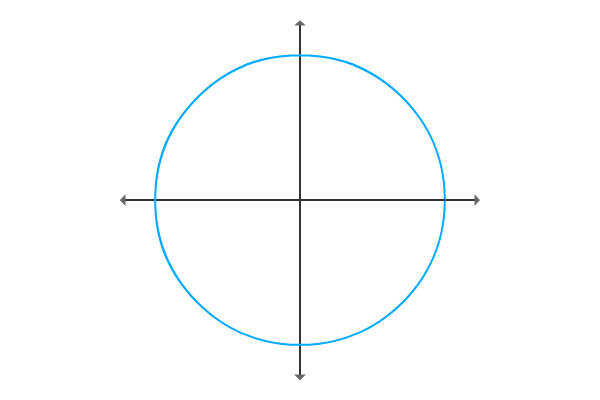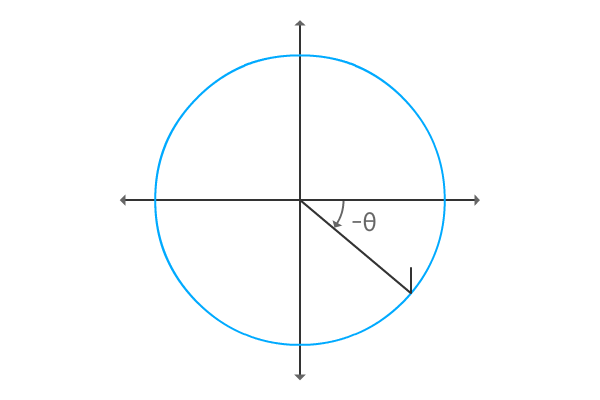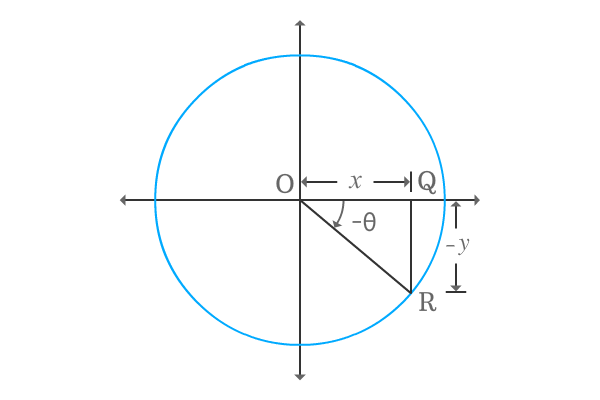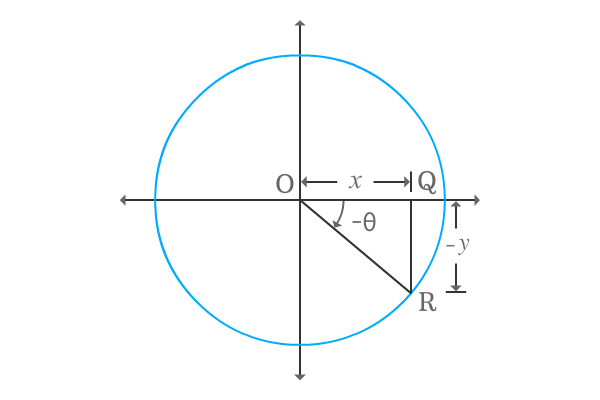
Construct the same triangle with negative angle. Therefore, the angle of $\Delta QOR$ is negative theta, denoted by $–\theta$.

On the basis of this data, write the tan of negative angle in terms of ratio of lengths of respective sides.

$\tan{(-\theta)} \,=\, \dfrac{QR}{OQ}$

Due to construction of the triangle with negative angle, geometrically the length of opposite side will be $–y$ but the length of adjacent side is same.

$\implies$ $\tan{(-\theta)} \,=\, \dfrac{-y}{x}$

Comparing Cosine functions

Now, compare equations of both tangent of positive angle and tan of negative angle.

$\tan{\theta} \,=\, \dfrac{y}{x}$

$\tan{(-\theta)} \,=\, -\dfrac{y}{x}$

The two equations disclose that tan of negative angle is always equal to negative of tangent of angle.

$\,\,\, \therefore \,\,\,\,\,\,$ $\tan{(-\theta)} \,=\, -\tan{\theta}$

It is called tangent of negative angle identity and used as a formula in trigonometric mathematics.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.