Natural Logarithm

A logarithmic system which contains neper constant ($e$) as its base, is called natural logarithm.

Introduction

John Napier, a Scottish mathematician who introduced logarithmic system firstly by an irrational mathematical constant $e$ (known as Napier constant).

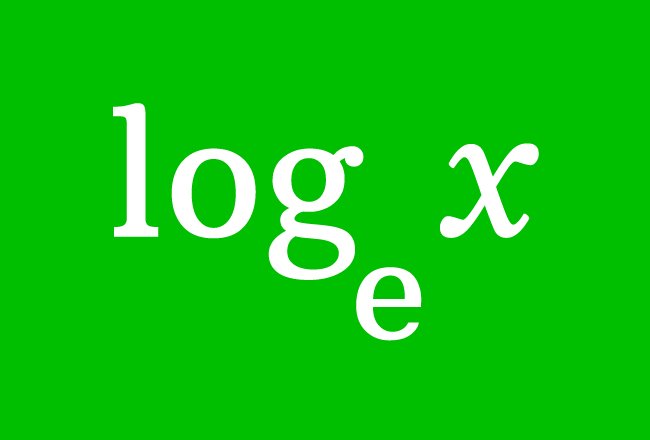
He split the quantities as multiplying factors on the basis of his neper constant $e$. Thus a natural logarithmic table was introduced and it made calculations like multiplication and division easier.

John Napier developed this logarithmic system in natural mathematical approach. Therefore, it is generally called as natural logarithm and also often called as Napier’s logarithms.

He defined the value of Napier constant as

$e \,=\, 2.718281828459\ldots$

Algebraic form

Logarithm is simply denoted by $\log$ symbol and $e$ is used as subscript of log to express that $e$ is a base of the logarithm.

Representation

If $q$ is a quantity, then logarithm of $q$ to base $e$ is written in mathematical form as $\log_{e}{q}$. It is also written as $\ln{q}$ simply.

Therefore, $\log_{e}{q}$ and $\ln{q}$ both represent natural logarithm of quantity $q$ in mathematics.

Inverse Operation

Natural Logarithm and Exponentiation are inverse operations. So, it is very important to know the relation between them.

The total number of multiplying factors is $x$ when the quantity $q$ is divided as multiplying factors on the basis of another quantity $e$.

$\log_{e}{q} \,=\, x$ then $q \,=\, e^{\displaystyle x}$

Therefore, $\log_{e}{q} \,=\, x$ $\, \Leftrightarrow \,$ $q \,=\, e^{\displaystyle x}$

It can also be written as

$\ln{q} \,=\, x$ $\, \Leftrightarrow \,$ $q \,=\, e^{\displaystyle x}$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.